Как движение дислокациЙ

Возьмем кубический образец (рис. 3.6, а) и сдвинем его верхнюю половину по плоскости АА на расстояние, равное параметру кристаллической решет­ки а (рис. 3.6, б). При этом длина образца увеличивается L ' = L + Δ L; Δ L ≈ a. Из состояния, показанного на рис. 3.6, а, в состояние рис.3.6, б можно перейти двумя способами:

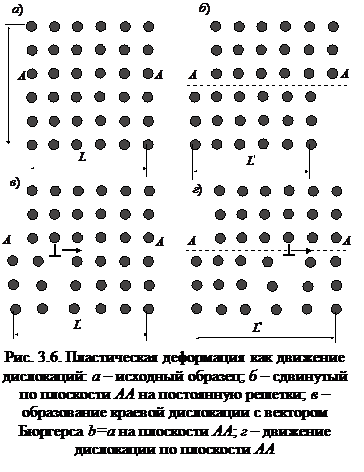- сдвинув одновременно всю верхнюю часть кристалла относительно нижней (для этого надо приложить скалывающее напряжение, равное теоретической прочности, см. главу 1;

- образовав на плоскости АА краевую дислокацию с век­тором Бюргерса b = а и продвинув ее с левого края кристалла на правый (рис. 3.6, в и г).

И в том и в другом случае удлинение кристалла одина­ково: L ₁≈ L + a. Постепенное перемещение дислока­ции с вектором Бюргерса b по какой-либо плоскости эквивалентно одновременному сдвигу одной части кристалла относительно другой на b вдоль плоскости скольжения дислока­ции.

Пластическая деформация при таком перемещении одной дислокации

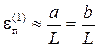, (3.1)

а при перемещении n дислокаций

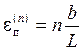. (3.2)

При движении по плоскости АА дислокация может пройти путь l < L и затормозиться на каком-либо препятствии. Вели­чина l в таком случае называется длиной свободного пробега дислокации, а сдвиг – незавершенным. В теории упругости показано, что при этом удлинение образца Δ L составляет (см. рис. 3.6, в, г):

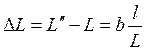. (3.3)

Аналогично при перемещении п дислокаций на l каждая

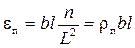, (3.4)

где ρ _п= n / L ² – плотность подвижных дислокаций – полное число дислокационных трубок, пересекающих единицу площади (1 м² или 1 см²) поверхности кри­сталла. Формула (3.4) играет большую роль в теории дислока­ций, связывая плотность подвижных дислокации ρ _п, их век­тор Бюргерса b, длину свободного пробега l и производимую ими пластическую деформацию ε _п.

Продифференцировав (3.4) по времени, получаем выражение для скорости пластической деформации :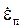

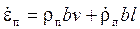, (3.5)

где v = dl/dt – скорость дислокаций, зависящая от напряже­ния; 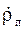– изменение плотности подвижных дислокации во времени. Если изменения напряжения в процессе пластиче­ской деформации невелики, то обычно 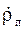мало и вторым чле­ном можно пренебречь, т. е.

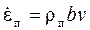. (3.6)

Это выражение называют часто соотношением Мотта-Хаазена. Оценим, исходя из (3.6), какую скорость деформации 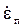можно достичь за счет дислокационного механизма деформации. При больших напряжениях подвижными могут стать почти все дислокации, тогда ρ _п ≈ ρ. Плотность дислокаций в деформированном металле может достигать 10¹⁴÷ 10¹⁶ 1/м², а их скорость не превышает скорости звука (3÷ 5)× 10³ м/с. Подставив ρ = 10¹⁵ м^–2, b = 3× 10^–10м, v =10³ м/с, получим 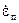≈ 3× 10⁸ с^–1, что соответствует удлинению тела вдвое за 3× 10^–9 с. Скорости деформации реальных технологических процессов редко превышают 10⁴ с^–1. Таким образом, можно заключить, что обычной плотности дислокаций вполне достаточно, чтобы обеспечить самые быстрые из существующих промышленных видов пластической деформации.

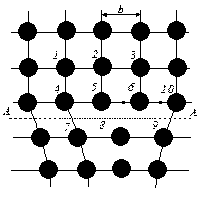
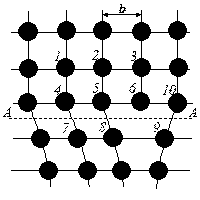
Рассмотрим движение краевой дислокации. На рис. 3.7, а изображено сечение простого кубического кристалла, содержащего краевую дислокацию с осью вдоль конца полуплоскости 3. Для простоты будем считать, что силы притяжения между атомами очень быстро уменьшаются с увеличением расстояния между ними. Поэтому связи между атомами 4-7 и 6-8 сильно ослаблены (рис. 3.7, а), а между атомами 5- 7 и 5-8 пренебрежимо малы (разорваны). Приложим к решетке касательное напряжение τ (рис. 3.7, б), которое приведет к перекосу решетки. Вследствие этого расстояние между атомами 6-8 увели­чится, а 5-8 – уменьшится. При увеличении τ сверх некоторого критического, связь 6-8 порвется (условно по линии АА), и атом 8 соединится с атомом 5. В результате полуплоскость 3 соединится с нижней полуплоскостью 4' и образует целую плоскость 34', а полуплоскость 4 станет «лишней». Конец этой полуплоскости (атом 6 в сечении) и будет теперь осью дис­локации (рис.3.7, в). Следовательно, можно считать, что дислокация переместилась на одно межатомное расстояние. Такое движение дислокации называется консервативным или скольжением.

а)	б)	в)
1 2 3 4 5	1 2 3 4 5	1 2 3 4 5
1′ 2′ 4′ 5′	1′ 2′ 4′ 5′	1′ 2′ 3 ¢ 5′
Рис. 3.7. Перемещение дислокации в плоскости скольжения

Существенные черты такого движения:

1. Дислокация перемещается в плоскости, включающей векторы b и l. Плоскость, проведенная через ось дислокации и вектор Бюргерса, называется поэтому плоскостью скольжения. Этим термином мы уже пользовались несколько раз, не расшифровывая его смысл.

2. Общее число разорванных связей (для простого кубического кристалла в нашем приближении две связи 5-7 и 5-8, рис. 3.7, а) после смещения дислокации на целое число шагов сохраняется. В рассмотренном выше примере после одного скачка остались две разорванные связи 6-8 и 6-9 (рис. 3.7, в). Именно сохранение общего числа разорванных (или сильно напряженных, если силы спадают не очень быстро) связей и делает такое движение дислокации обратимым.

3. Краевые дислокации имеют одну плоскость скольжения: через две пересекающиеся прямые (ось дислока­ции и вектор Бюргерса) можно провести одну и только одну плоскость. Винтовая дислокация имеет столько плоскостей скольжения, сколько через нее можно провести кристаллографических плоскостей, т. е. число плоскостей скольжения зави­сит от ее ориентации и от типа кристаллической решетки. Реально винтовая дислокация может перемещаться по (2÷ 4) плоскостям скольжения.

4. Движение дислокации в плоскости скольжения напоми­нает эстафетное движение, в котором каждый из бегунов про­бегает малую часть всей дистанции, а весь путь проходит только эстафетная палочка.

Всякое движение дислокации под углом к плоскости скольжения называется неконсервативным или переполза­нием. Этот механизм перемещения дислокации, сопровождающийся испусканием вакансий, рассмотрен в разделе 2.6. Процесс переползания связан с диффузией больших групп вакансий или внедренных атомов, поэтому переползание - медленный процесс, сильно зависящий от температуры.

5. Из-за низкой скорости переползания ее непосредственный вклад в скорость деформации мал: 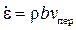, где v _пер – средняя скорость переползания дислокации. Эта формула аналогична (3.6). Исключением является движение винтовой дислокации со ступеньками (рис. 3.8). Рассмотрим его.

Пусть в простой кубической решетке есть дислокация с ломаной линией, состоящая из длинных l _в > > а отрезков винтовой ориентации и коротких l _к~ a отрезков краевой дислокации. Движение в направлении х требует переползания краевых отрезков. Но поскольку перемещение всех их на расстояние а приводит к такому же перемещению всей дислокации, то эффективная скорость дислокации увеличивается в l _в /l _к раз. Действитель­но, если поглощение п вакансий в секунду на 1 м длины чисто краевой дислокации приводит к ее скорости

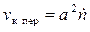.[В. В.1] (3.7)

(дислокация совершает 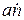перескоков в секунду, каждый из перескоков равен а), то для смешанной дислокации

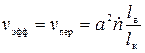. (3.8)

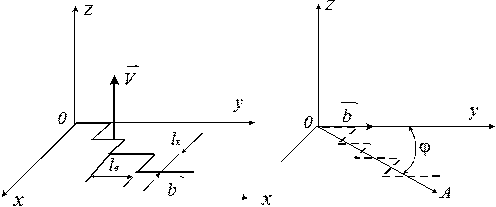
Рис. 3.8. Движение винтовой дислокации со ступеньками: а – истинная конфигурация; б – эффективная конфигурация

Поскольку вакансии необходимы только для перескоков крае­вых участков, их частота возрастает в l _в /l _к раз. Правда, для этого необходимо предположение, что все вакансии, попадающие на дислокацию, в итоге оказываются на краевых участках. Точно такое же движение смешанной дислокации может происходить с помощью испускания внедренных ато­мов.

При недостаточно большом увеличении смешанная дисло­кация (рис. 3.8, а) выглядит прямолинейной (рис. 3.8, б), но с вектором Бюргерса b, расположенным под малым углом φ (tgφ = l _к /l _в) к оси дислокации. Тогда можно записать

v _эфф = v _персtgφ.

6. Переползание играет важную роль при преодолении дислокацией препятствий в плоскости скольжения. Это происходит при температурах деформации, при которых диффузия вакансий происходит достаточно эффективно. Пусть крае­вая дислокация встречает расположенные равномерно препятствия А размером r и рас­стоянием между ними l в плоскости ее скольжения (рис. 3.9). Повторяя предыдущие рассуждения, получим, что скорость дислокации

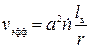. (3.9)

Так как r обычно порядка нескольких а, то v _эфф> > v _{к пер}. Переползание играет при этом механизме вспомогательную роль, освобождая дислокацию от препятствий, а основной вклад (как и в случае движения винтовой дислокации со сту­пеньками) в пластическую деформацию вносит скольжение.

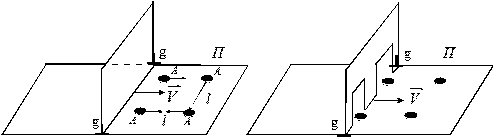
Рис. 3.9. Движение дислокации gg в плоскости скольжения П, содержащей препятствия А, путем их переползания: а – исходное положение; б – переползание отрезков дислокации вблизи препятствий, обеспечивающее их свободное движение

Таким образом, существуют два типа движения дислока­ции: быстрый – скольжение и медленный – переползание, причем переползание играет существенную роль обычно только тогда, когда скольжение дислокации по каким-либо причинам затруднено.