
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
По кристаллической решетке некоторых металлов
|
|
| Величина | Металл | ||||||
| Si | Ge | Bi | Fe | Сu | Ag | Al | |
| W пер0, эВ | 2, 2 | 1, 5 | 0, 31 | 0, 2 | 0, 1 | 0, 085 | 0.09 |
| τ п, МПа | 0, 135 | 0, 13 | 0, 075[В3] | ||||
| W П1, эВ | 0, 45 | 0, 23 | 0, 01 | 0, 004 | 0.001 | 0, 0007 | 0, 0008 |
| Тип связи | Ковалентный | Смешанный | Металлический |
П р и м е ч а н и е. W П1≈ W П b – энергия барьера Пайерлса на одну атомную плоскость.
5. Дислокация обладает высокой подвижностью, если ее плоскость скольжения (плоскость, проведенная через ось дислокации и вектор Бюргерса) совпадает с какой-либо плоскостью легкого скольжения, а ее вектор Бюргерса минимальный из всех возможных. Наоборот, если плоскость скольжения дислокации такова, что для нее отношение а/b очень мало, то τ П для нее велико и дислокация является практически неподвижной или, как часто говорят, сидячей.
6. При прочих равных условиях краевые дислокации всегда более подвижны, чем винтовые. Действительно, согласно условиям, сформулированным в п. 2, при а/b= 1 для краевых дислокации τ кП ≈ 2, 5ּ 10–4 G, а для винтовых τ вП≈ 4ּ 10–3 G. Это обстоятельство должно быть наиболее существенно для кристаллов с высоким барьером Пайерлса W П.
Итак, мы получили очень важные качественные результаты, такие, как наличие плоскостей легкого скольжения, зависимость напряжения Пайерлса τ П от величины вектора Бюргерса, типа дислокации, характера связей между атомами и типа кристаллической решетки.
 3.5. Напряжения от дислокации
3.5. Напряжения от дислокации
Рассмотрим напряжения от винтовой дислокации, рис.3.12. Пусть ось винтовой дислокации направлена вдоль оси z. Выберем какую-либо точку 1, расположенную на расстоянии r от оси, и опустим из нее на ось перпендикуляр, приняв точку пересечения за начало координат 0. Построим контур Бюргерса, начинающийся в точке 1. Тогда его конечная точка 2 будет лежать в плоскости 10z (проходящей через ось z и точку 1) и отстоять от точки 1 на вектор Бюргерса дислокации b. Проведем радиусы-векторы ко всем точкам контура. Начальный радиус-вектор 01 будет перпендикулярен 0z, конечный после поворота на 2π 02 наклонен под углом  к 01 и углом
к 01 и углом 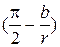 к оси. Так как все радиус-векторы у винтовой дислокации равноправны, то наклон ω должен меняться плавно от 0 до b/r при изменении θ от 0 до 2π, т. е. ω (θ)=
к оси. Так как все радиус-векторы у винтовой дислокации равноправны, то наклон ω должен меняться плавно от 0 до b/r при изменении θ от 0 до 2π, т. е. ω (θ)= 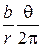 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Относительная деформация решетки ε характеризуется скоростью изменения смещения координаты i при изменении координаты k. Из предыдущего рассуждения видно, что в случае винтовой дислокации имеются только смещения в направлении z, меняющиеся при изменении θ, т.е.
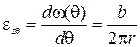 .
.
От деформации перейдем к напряжению: τ z θ = G ε z θ , где G – модуль сдвига. Отсюда
τ zθ = 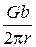 . (3.13)
. (3.13)
Из условия равновесия τ θ z = τ z θ . В силу симметрии по углу θ напряжения зависят только от модуля r. Основной характеристикой внутренних напряжений является закон их уменьшения при удалении от источника. Из (3.13) видно, что τ θ z = τ z θ ~1/ r. Таким образом, дислокации являются источниками дальнодействующих внутренних напряжений.
b декартовой системе координат напряжения вблизи винтовой дислокации равны:
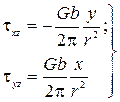 (3.14)
(3.14)
Напряжения вблизи краевой дислокации (рис. 3.13):
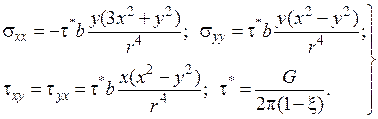 (3.15)
(3.15)
Выразив х и у через r и угол θ, можно получить, что напряжения пропорциональны 1/ r. Таким образом, закон изменения напряжений при удалении от краевой дислокации такой же, как и для винтовой дислокации.
Отметим, что вблизи ядра (r»b) дислокации создают очень большие напряжения, по величине близкие к теоретической прочности кристалла t*.
|
|
