💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Точечные оценки

Определение. Статистической оценкой Q^* неизвестного параметра Q теоретического распределения называют функцию f(x₁, x₂, …, x_n) от наблюдаемых случайных значений x₁, x₂, …, x_n.

Определение. Точечной оценкой называют статистическую оценку, которая определяется одним числом Q^* = f(x₁, x₂, …, x_n), где x₁, x₂, …, x_n ─ результаты n наблюдений над количественным признаком Х (выборка).

Определение. Несмещенной называют точечную оценку Q^*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, то есть M(Q^*) = Q. Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру.

Выборочная средняя.

Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.

Определение. Выборочной средней 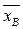называют среднее арифметическое значение признака выборочной совокупности.

Если все значения x₁, x₂, …, x_n признака выборки объема n различны, то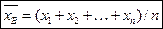

Если же все значения признака x₁, x₂, …, x_k имеют соответственно частоты n₁, n₂, …, n_k, причем n₁ + n₂ + … + n_k = n, то

,

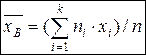где 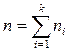– объем выборки.

Выборочная средняя является несмещенной оценкой генеральной средней (неизвестного математического ожидания).

Замечание. Если первоначальные варианты 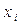─ большие числа, то для упрощения решения целесообразно вычесть из каждой варианты одно и то же

число С, то есть перейти к условным вариантам u_i = x_i – c. Тогда

.
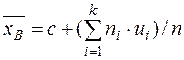