💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Интервальные оценки

Определение. Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной вероятностью (надежностью) γ покрывает заданный параметр.

Интервальной оценкой (с надежностью γ) математического ожидания a нормально распределенного признака Х по выборочной средней 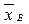при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал

,

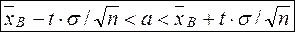где = δ – точность оценки,

n – объем выборки,

t – значение аргумента функции Лапласа Ф(t) (см. приложение 2). при котором Ф(t)=γ /2.

При неизвестном σ (и объеме выборки n< 30) доверительным будет интервал

,

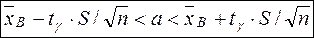где S – «исправленное» выборочное среднее квадратическое отклонение,

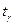находят по таблице приложения 3 по заданным n и γ.

Интервальной оценкой (с надежностью γ) среднего квадратического отклонения σ нормально распределенного количественного признака Х по «исправленному» выборочному среднему квадратическому отклонению S служит доверительный интервал:

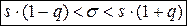
при q< 1,

0 < σ < s∙ (1 + q)

при q > 1,

где q находят по таблице приложения 4 по заданным n и γ.

Интервальной оценкой (с надежностью γ) неизвестной вероятности р биноминального распределения по относительной частоте w служит доверительный интервал (с приближенными концами p₁ и p₂)

,

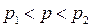где ,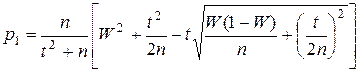

.

где n – общее число испытаний,

m – число появлений события.

W – относительная частота, равная отношению m/n;

t – значение аргумента функции Лапласа (приложение 2), при котором Ф(t)=γ /2 (γ – заданная надежность).

Замечание. При больших значениях n (порядка сотен) можно принять в качестве приближенных границ доверительного интервала

,

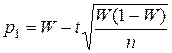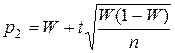
Пример 1. Из генеральной совокупности извлечена выборка объема n = 9:

Варианта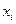
Частота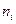

Оценить с надежностью 0, 95 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.

Решение. Выборочную среднюю и «исправленное» среднее квадратическое отклонение найдем соответственно по формулам

, .

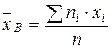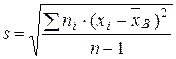Подставим в эти формулы данные задачи:

.

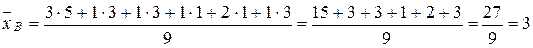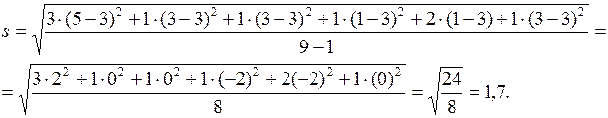
Таким образом, получим 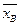=3, s = 1, 7.

Найдем искомый доверительный интервал:

.

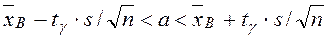Значение 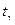находят по таблице приложения 3 по заданным n = 9 и γ =0, 95: 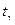=2, 31.

Подставляя 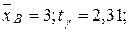s = 1, 7; n = 9; получим

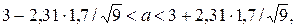
1, 691 < a < 4.309.

Получили доверительный интервал (1, 7; 4, 3), покрывающий неизвестное математическое ожидание а с надежностью γ = 0, 95.

Пример 2. По данным выборки объема n = 40 из генеральной совокупности найдено «исправленное» среднее квадратическое отклонение s =1 нормально распределенного количественного признака. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0, 99.