Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Числовые характеристики дискретной случайной величины

Определение. Математическим ожиданием дискретной случайной величины М(Х) называется число, равное сумме произведений значений случайной величины на соответствующие вероятности их появления:

М(Х) = x₁ ∙ p₁ + x₁ ∙ p₁ + … + x_n ∙ p_n

Математическое ожидание обладает следующимисвойствами:

1. Математическое ожидание постоянной величины равно самой постоянной:

М(С) = С.

2. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых (то же относится к разности):

М(Х ± У) = М(Х) ± М(У).

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

М(Х∙ У)=M(Х) ∙ M(У).

4. Постоянный множитель можно выносить за знак математического ожидания:

М(С∙ Х)=С∙ М(Х).

Определение. Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(Х)=M[Х–M(Х)]².

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:

D(Х)=M(Х²)–[M(Х)]².

Доказательство. Математическое ожидание М(Х) есть постоянная величина, следовательно, 2∙ М(Х) и М² (Х) есть также постоянные величины. Приняв это во внимание и пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), упростим формулу, выражающую определение дисперсии:

D(X) = M[X–M(X)]² = M[X² – 2∙ X∙ M(X)+M² (X)] = M(X²)–2∙ M(X)∙ M(X)+M² (X) =

=M(X²) – 2M² (X) + M² (X) = M(X²) – M² (X).

Итак,

D(X) = M(X²) – [M(X)]².

Квадратная скобка введена в запись формулы для удобства ее запоминания.

Свойства дисперсии:

1. Дисперсия постоянной равна нулю:

D(C) = 0.

2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

D(C∙ X)=C² ∙ D(X).

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

D(X + Y) = D(X) + D(Y).

4. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:

D(X + С) = D(X).

Пример1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения:

Решение. Найдем математическое ожидание Х:

М(Х) = –5 ∙ 0, 4 + 2 ∙ 0, 3 + 3 ∙ 0, 1 + 4 ∙ 0, 2 = – 0, 3.

Дисперсию можно вычислить, исходя из ее определения, однако воспользуемся формулой:

D(X) = M(X²) – [M(X)]²,

которая быстрее ведет к цели.

Напишем закон распределения Х²:

Найдем математическое ожидание Х²:

М(Х²) = 25 ∙ 0, 4+4 ∙ 0, 3+9 ∙ 0, 1+16 ∙ 0, 2 = 15, 3.

Найдем искомую дисперсию:

D(X) = M(X²) – [M(X)]² = 15, 3 – (–0, 3)² = 15, 21.

Найдем искомое среднее квадратическое отклонение:

σ (Х) = 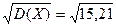=3, 9.

Определение. Дискретная случайная величина Х, вероятности значений которой находятся по формуле Бернулли, называется распределённой по биномиальному закону. В таком случае говорят, что Х имеет биномиальное распределение.

Теорема.

Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины Х, распределённой по биномиальному закону, вычисляются по формулам:

М(Х) = n∙ p, D(X) = n∙ p∙ q, s(X) = ,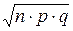

где n – число испытаний;

р – вероятность появления события

q – вероятность непоявления события.