Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Эмпирическая функция распределения

Пусть известно статистическое распределение частот количественного признака Х. Введем обозначения: 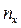─ число наблюдений, при которых наблюдалось значение признака, меньше х; n – общее число наблюдений (объем выборки). Ясно, что относительная частота события Х< х равна 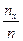. Если х изменяется, то, вообще говоря, изменится и относительная частота, то есть относительная частота 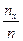есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Определение. Эмпирическая функция распределения (функция распределения выборки) – функция F^*(x), определяющая для каждого значения х относительную частоту события X< x.

,

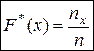где 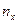─ число вариант, меньших х; n – объем выборки.

Например, для того чтобы найти F^*(x₂), надо число вариант, меньших x₂, разделить на объем выборки:

.

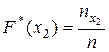В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(x) определяет вероятность события X< x, а эмпирическая функция F^*(x) определяет относительную частоту этого же события.

Из теоремы Бернулли следует, что относительная частота события X< x, то есть F^*(x), стремится по вероятности к вероятности этого события, то есть к значению F(x). Другими словами, при больших значениях n числа F^*(x) и F(x) мало отличаются одно от другого в том смысле, что 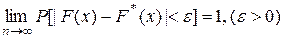. Уже отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности. Такое заключение подтверждается и тем, что F^*(x) обладает всеми свойствами F(x).

Из определения функции F^*(x) вытекают следующие ее свойства:

1) Значения эмпирической функции принадлежит отрезку [0; 1];

2) F^*(x) – неубывающая функция;

3) Если x₁ ─ наименьшая варианта, то F^*(x) = 0 при х < х₁;

если х_k ─ наибольшая варианта, то F^*(x) = 1 при х > x_k.

Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример. Построить эмпирическую функцию по данному распределению выборки:

Варианты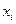
Частоты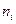

Решение. Найдем объем выборки (сумма всех частот n_i):

n = n₁ + n₁ + n₁ = 12 + 18 + 30 = 60.

Наименьшая варианта равна 2 (x₁ = 2), следовательно, F^*(x) = 0 при х ≤ 2 (по свойству 3 функции F^*(x));

значения, меньшие 6 (х< 6), а именно x₁ = 2, наблюдались n₁ = 12 раз, следовательно, при 2< x≤ 6;

значения х< 10, а именно x₁ = 2, x₁ = 2 наблюдались n₁ + n₂ = 12 + 18 = 30 раз, следовательно 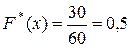при 6< х≤ 10.

Так как х =10 – наибольшая варианта, то F^*(x) = 1 при х> 10 (по свойству 4 функции F^*(x)).

Искомая эмпирическая функция имеет вид:

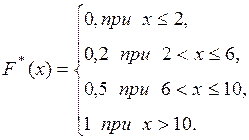
Ниже приведен график полученной эмпирической функции.

На графике на соответствующих осях откладывают значения функции F^*(x) и интервалы вариант

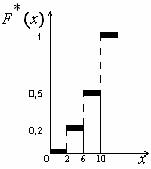
Рис. 5. График эмпирической функции.