
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальное распределение. Определение. Случайная величина Х имеет нормальный закон распределения, если ее функция плотности вероятности имеет вид:
|
|
Определение. Случайная величина Х имеет нормальный закон распределения, если ее функция плотности вероятности имеет вид:
f(x)= 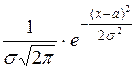 ,
,
где σ и a – параметры распределения.
Определение. График функции f(x) называется нормальной кривой или кривой нормального распределения.
Методами дифференциального исчисления можно установить, что:
1. кривая симметрична относительно прямой х= a;
2. функция имеет максимум при х= a f(a)= 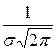 ;
;
3. по мере удаления х от точки a функция убывает и при х→ 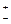 ∞ кривая приближается к оси Ох;
∞ кривая приближается к оси Ох;
4. кривая выпукла вверх при х є (a – σ; a + σ) и
выпукла вниз при х є (– ∞; a – σ) и х є (a + σ; + ∞).
|
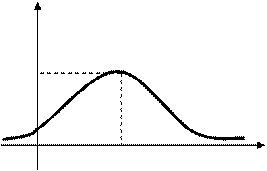
Рис. 4. Кривая нормального распределения.
Замечание. Форма кривой изменяется с изменением параметра σ. С возрастанием σ кривая f(x) становится более пологой и растянутой вдоль оси Ох.
Значениям случайной величины, близким к математическому ожиданию, соответствует большая плотность вероятности, то есть малые отклонения значений случайной величины от ее математического ожидания встречаются чаще, чем большие.
Так как случайная величина определена на всей числовой оси, то при вычислении числовых характеристик рассматривается интеграл на промежутке (– ∞; +∞). Можно показать, что:
М(Х) = 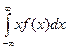 =
= 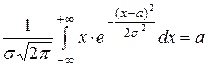 ,
,
D(Х)= 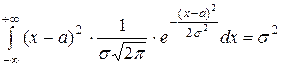 ,
,
σ (Х) = σ.
Свойства нормального распределения.
1. Вероятность того, что нормально распределенная случайная величина Х примет значение, принадлежащее интервалу (α; β), находится по формуле:
Р(α < Х < β) = Ф 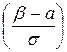 —Ф
—Ф 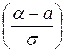 ,
,
где Φ (х) 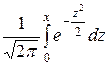 – функция Лапласа (см. приложение 2).
– функция Лапласа (см. приложение 2).
2. Вероятность того, что абсолютная величина отклонения меньше положительного числа δ находится по формуле:
Р(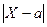 < δ)=2Ф(
< δ)=2Ф(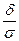 ).
).
В частности при a =0 справедливо равенство:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Р(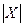 < δ)= 2Ф(
< δ)= 2Ф(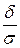 ).
).
Правило «3 σ».
Для нормально распределенной случайной величины велика вероятность того, что при однократном испытании отклонение величины от ее математического ожидания не превышает среднего квадратического отклонения.
Преобразуем формулу Р(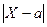 < δ)=2Ф(
< δ)=2Ф(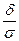 ), положив δ =σ ·t. В итоге получим
), положив δ =σ ·t. В итоге получим
Р(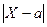 < σ ·t)=2Ф(t).
< σ ·t)=2Ф(t).
Если t=3 и, следовательно, σ ·t=3σ, то 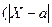 <
< 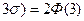 =
=  , то есть вероятность того, что отклонение от математического ожидания по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0, 9973. Это и есть правило «3 σ».
, то есть вероятность того, что отклонение от математического ожидания по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0, 9973. Это и есть правило «3 σ».
Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0, 0027.
Это означает, что лишь в 0, 27% случаев так может произойти, что значения нормально распределенной случайной величины выйдут за пределы интервала (a – 3σ; a + 3σ). Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможным. В этом и состоит сущность правила трех сигм.
 Пример 1.Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х равны соответственно 11 и 4. Найти вероятность того, что в результате испытания Х примет значение, заключенного в интервале (19; 23).
Пример 1.Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х равны соответственно 11 и 4. Найти вероятность того, что в результате испытания Х примет значение, заключенного в интервале (19; 23).
Решение. Воспользуемся формулой:
Р(α < Х< β)=Ф 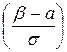 —Ф
—Ф 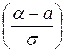 .
.
По условию, α = 19; β = 23; а = 11; σ = 4, тогда
Р(19< Х< 23)=Ф 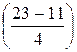 – Ф
– Ф  = Ф(3) – Ф(2).
= Ф(3) – Ф(2).
По таблице приложения 2 находим: Ф(3)=0, 49865, Ф(2)=0, 4772.
Найдем искомую вероятность (вероятность того, что в результате испытания Х примет значение, заключенное в интервале (19; 23)):
Р(19< Х< 23)=0, 49865 – 0, 4772=0, 02145.
Пример 2. Математическое ожидание нормально распределенной случайной величины Х равно 5 и среднее квадратическое отклонение равно 2. Написать плотность вероятности Х.
Решение. Плотность нормально распределенрон случайной величины Х имеет вид:
f(x)= 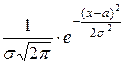 .
.
Подставив a =5 и σ =2, получим:
f(x)= 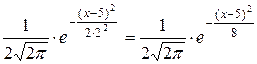 .
.
§13. Статистическое распределение выборки
Пусть для изучения количественного (дискретного или непрерывного) признака Х из генеральной совокупности извлечена выборка, причем значение x1 наблюдалось n1 раз, значение x2 наблюдалось n2 раз, …, значение xk наблюдалось nk раз.
Наблюдаемые значения xi (i = 1, 2, …, n) признака Х называют вариантами, а последовательность всех вариант, записанных в возрастающем порядке, – вариационным рядом. Числа наблюдений ni называют частотами, их сумма 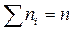 ─ объем выборки. Отношения частот к объему выборки
─ объем выборки. Отношения частот к объему выборки 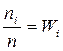 ─ относительными частотами.
─ относительными частотами.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Статистическим распределением выборки называют перечень вариант xi вариационного ряда и соответствующих им частот ni (сумма всех частот равна объему выборки n) или относительных частот Wi (сумма всех относительных частот равна единице). Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами (или относительными частотами).
Пример. Задано распределение частот выборки объема n = 20:
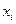
| |||
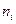
|
В данной выборке получены следующие варианты x1 = 2; x2 = 6; x3 = 12,
соответствующие частоты n1 = 3; n2 = 10; n3 = 7.
Напишем распределение относительных частот.
Решение. Найдем относительные частоты, для чего разделим частоты на объем выборки 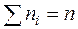 = 3 + 10 + 7 = 20.
= 3 + 10 + 7 = 20.
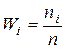 ─ относительные частоты:
─ относительные частоты:
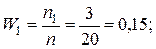
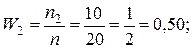
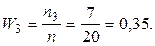
Напишем распределение относительных частот:
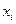
| |||
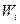
| 0, 15 | 0, 50 | 0, 35 |
Контроль: сумма всех относительных частот 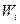 равна единице:
равна единице:
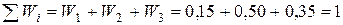 .
.
|
|

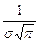 0 a X
0 a X