Разомкнутая семо с неоднородным потоком заявок

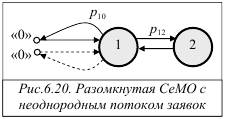Положим, что в линейную разомкнутую СеМО с двумя узлами поступает неоднородный поток заявок двух классов (рис.6.20). Заявки класса 1 (сплошная линия) и класса 2 (пунктирная линия) поступают в узел 1 и образуют простейшие потоки со средними интервалами 100 и 50 секунд соответственно. После обслуживания в узле 1 заявки класса 1 с вероятностью p₁₂ = 0, 8 переходят на обслуживание в узел 2 и с вероятностью p₁₀ = 0, 2 покидают СеМО. Заявки класса 2 обслуживаются только в узле 1, после чего покидают СеМО.

Длительности обслуживания заявок класса 1 и 2 в двухканальном узле 1 представляют собой равномерно распределённые случайные величины в интервалах (15±5) и (10 ±5) секунд соответственно.

Длительность обслуживания заявок класса 2 в одноканальном узле 2 – величина случайная, распределенная по экспоненциальному закону со средним значением 20 секунд.

Краткое описание рассматриваемой СеМО:

• количество потоков (классов) заявок: H = 2;

• количество узлов в сети: n = 2;

• количество обслуживающих приборов в узле 1: K₁ = 2;

• количество обслуживающих приборов в узле 2: K₂ =1;

• емкость накопителей в узлах сети – не ограничена, то есть в сети не может быть потерь заявок, что обусловливает линейность сети;

• потоки заявок класса 1 и класса 2 – простейшие;

• средний интервал между поступающими заявками класса 1:

a₀(1)= 100c;

• средний интервал между поступающими заявками класса 2:

a₀(2)= 50c;

• длительность обслуживания заявок класса 1 в узле 1 распределена равномерно в интервале от 10 до 20 с: b₁(1) =15 ± 5 c;

• длительность обслуживания заявок класса 2 в узле 1 распределена равномерно в интервале от 5 до 15 с: b₁(2) =10 ± 5 c;

• длительность обслуживания заявок класса 1 в узле 2 распределена по экспоненциальному закону со средним значением 20 с: b₂(1)= 20c.

Текст GPSS-модели разомкнутой СеМО с неоднородным потоком заявок представлен на следующей странице.

В рассматриваемой GPSS-модели, в отличие от модели 5 двухузловой РСеМО с однородным потоком заявок, появился третий модуль, моделирующий процессы поступления и обслуживания заявок класса 2 в узле 1.

Таким образом, при моделировании СеМО с неоднородным потоком заявок количество исполняемых модулей GPSS-модели определяется как произведение количества классов заявок на количество узлов моделируемой СеМО.

Анализ представленного отчета позволяет получить основные характеристики функционирования разомкнутой СеМО с неоднородным потоком заявок (наиболее интересные и важные результаты моделирования выделены жирным шрифтом).

ВЫВОД

При моделировании СеМО с неоднородным потоком заявок количество исполняемых модулей GPSS-модели определяется как произведение количества классов заявок на количество узлов моделируемой СеМО.

GPSS-ОТЧЁТ МОДЕЛИРОВАНИЯ

На рис 6.21 представлен отчет с результатами имитационного моделирования разомкнутой СеМО с двумя классами заявок для значения 1000000 операнда А в команде START, заданного при запуске процесса моделирования.

В процессе моделирования через разомкнутую СеМО прошло N=0 1 000000 заявок обоих классов. Все обслуженные заявки попали в два блока TERMINATE и были удалены из модели.

По количеству транзактов каждого класса, прошедших через соответствующие блоки ENTER, SEIZE и TERMINATE можно рассчитать коэффициенты передач для заявок класса 1 (α ₁(1), α ₂(1)) и 2 (α ₁(2), α ₂(2)) в узлах 1 и 2 разомкнутой СеМО соответственно:

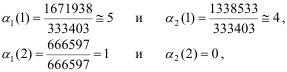
что соответствует теоретическим значениям, которые могут быть рассчитаны путём решения системы линейных алгебраических уравнений (4.16), как это описано в п.4.4.2.

Загрузки узлов СеМО (UTIL.) равны: ρ ₁ = 0, 476 и ρ ₂ = 0, 802.

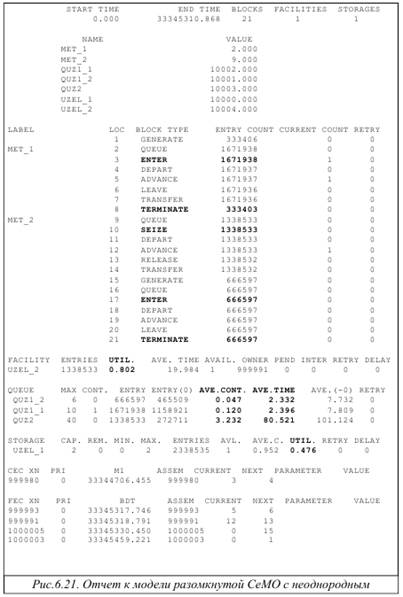
Среднее число заявок класса 1 в очереди (AVE.CONT.) в узлах 1 и 2 СеМО: l₁(1) = 0, 120 и l₂(1) = l₂ = 3, 232. Среднее число заявок класса 2 в очереди узла 1 СеМО: l₁(2) = 0, 047. Заметим, что в узле 2 очередь образуют только заявки первого класса. Суммарная длина очереди заявок в узле 1 равна l₁ = l₁(1) + l₁(2) = 0, 167. Суммарное число заявок, находящихся в состоянии ожидания в СеМО: L = l₁ + l₂ ≅ 3, 4.

Средние времена ожидания (AVE.TIME) заявок класса 1 в узлах 1 и 2 СеМО соответственно равны: w₁(1) = 2, 4с и w₂(1) = 80, 5с. Среднее время ожидания заявок класса 2 в узле 1 СеМО: w₁(2) = 2, 33с.

Следует заметить, что стандартный GPSS-отчёт по результатам моделирования содержит информацию не по всем характеристикам, которые могут представлять интерес для исследователя. В частности, представленный выше отчёт не содержит информацию о временах пребывания заявок в узлах и в СеМО в целом.

Эти характеристики могут быть рассчитаны на основе имеющихся в отчёте данных с использованием фундаментальных соотношений, представленных в п.3.4.3. Так, например, легко могут быть рассчитаны средние времена пребывания заявок каждого класса в узлах СеМО:

u₁(1) =w₁(1) +b₁(1)= 17, 4с; u₂(1) = w₂(1) + b₂(1) ==100, 5с;

u₁(2) =w₁(2)+b₁(2)= 12, 3с.

С учётом того, что за время нахождения в сети заявки класса 1 в среднем пройдут через узел 1 α ₁(1) = 5 раз, а через узел 2 – α ₂(1) = 4 раза, можно найти среднее время пребывания заявок класса 1 в сети:

U₁=α ₁(1)u₁(1) +α ₂(1)u₂(1)= 489с.

Аналогично, среднее время пребывания в сети заявок класса 2:

U₂=α ₁(2)u₁(2) +α ₂(2)u₂(2)= 12, 3с

Среднее число заявок каждого класса в СеМО может быть найдено по формулам Литтла, связывающим безразмерные и временные сетевые характеристики:

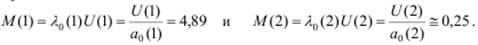
Для получения дополнительных результатов, например в виде гистограмм плотностей распределений времён ожидания и пребывания заявок в СеМО с целью детального анализа свойств исследуемой системы, в область описания GPSS-модели следует включить команды TABLE и QTABLE:

Для двух последних таблиц TU_k1 и TU_k2, в которых накапливается статистика по временам пребывания заявок обоих классов в СеМО, дополнительно в GPSS-модель необходимо вставить два оператора:

Первый оператор должен быть вставлен в модуль 1 перед оператором TERMINATE для отметки времени выхода из СеМО заявки класса 1, а второй – в модуль 3 перед оператором TERMINATE для отметки времени выхода из СеМО заявки класса 2.

В этом случае кроме средних значений временных характеристик могут быть получены значения среднеквадратических отклонений соответствующих характеристик:

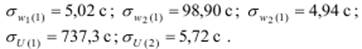
ВЫВОД

Стандартный GPSS-отчёт по результатам моделирования содержит информацию не по всем характеристикам, которые могут представлять интерес для исследователя. Эти характеристики могут быть рассчитаны на основе имеющихся в отчёте данных с использованием фундаментальных соотношений.