Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Расчет коэффициентов передач и интенсивностей потоков заявок в узлах РСеМО

Покажем, что интенсивности λ ₀, …, λ _n потоков заявок, поступающих в узлы 0,..., n сети, однозначно определяются вероятностями передач p_ij (i, j=1, …, n), задающими маршруты заявок в СеМО.

Будем рассматривать только установившийся режим.

Так как в линейной СеМО заявки не размножаются и не теряются, то интенсивности входящего и выходящего потоков для любого узла будут равны между собой.

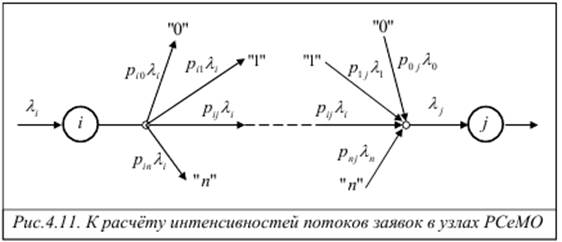
Интенсивность потока заявок, входящих в любой узел j сети, равна сумме интенсивностей потоков заявок, поступающих в него из других узлов i = 0, n (рис.4.11). Поскольку заявки из узла i поступают в узел j с вероятностью p_ij, то интенсивность потока заявок, поступающих из i в j, равна p_ijλ _i, где λ _i - интенсивность выходящего и, следовательно, входящего потока заявок узла i. С учетом этого, на входе узла j имеется поток с интенсивностью

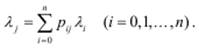(4.16)

Выражение (4.16) представляет собой систему линейных алгебраических уравнений (n +1)-го порядка, из которой могут быть найдены интенсивности потоков заявок в виде соотношения λ _j = α _jλ ₀ (j =1, n). Коэффициент α _j называется коэффициентом передачи и определяет среднее число попаданий заявки в узел j за время ее нахождения в сети, причем α ₀ =1.

Для разомкнутой СеМО известна интенсивность источника заявок λ ₀. Можно показать, что система уравнений для расчета интенсивностей имеет единственное решение вида λ _j = α _j λ ₀, где λ ₀ – заданная величина.