💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Расчет характеристик ЗСеМО

Характеристики ЗСеМО могут быть рассчитаны с использованием марковских процессов, поскольку количество состояний марковского процесса, в отличие от РСеМО, не бесконечно и равно числу сочетаний 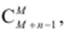, где n – число узлов в ЗСеМО и M – число заявок, циркулирующих в ЗСеМО. При этом основная трудность заключается в определении вероятностей состояний сети P(M₁, …, M_n) в случае большой ее размерности (n5>; M> 5), когда число состояний оказывается значительным. При выполнении расчетов на ЭВМ это, во многих случаях, приводит к потере значимости в процессе промежуточных вычислений и, следовательно, к невозможности получения конечных результатов.

От указанного недостатка свободен метод средних значений, позволяющий вычислять средние характеристики функционирования экспоненциальных СеМО на основе сравнительно простых рекуррентных соотношений.

Положим, что замкнутая однородная СеМО содержит n одноканальных узлов, длительности обслуживания заявок в которых распределены по экспоненциальному закону со средними значениями b₁, …, b_n соответственно. Пусть для каждого узла i сети известно среднее число попаданий заявки в данный узел за время ее нахождения в сети, то есть коэффициент передачи α _i, который, если конфигурация сети задана матрицей вероятностей передач P = [ p_ij | i, j = 0, 1, …, n], определяется в результате решения системы линейных алгебраических уравнений (4.17).

Обозначим: u_i - среднее время пребывания заявки в узле i за время пребывания в сети; m_i – среднее число заявок в узле i (i = 1, …, n); λ ₀ – производительность замкнутой сети. Очевидно, что эти величины зависят от числа заявок M, циркулирующих в замкнутой сети, то есть u_i = u_i (M); m_i = m_i (M); λ ₀ = λ ₀(M).

Можно показать, что имеют место следующие соотношения:

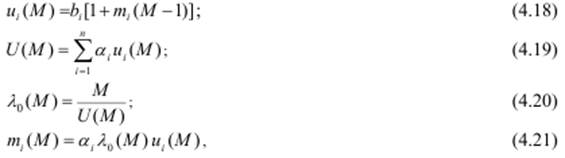
где U(M) – среднее время пребывания заявок в сети при условии нахождения в ней M заявок; m_i(0) = 0.

Выражение (4.18) получено на основе так называемой теоремы о прибытии [1], утверждающей, что в замкнутой экспоненциальной сети с одноканальными узлами, в которой циркулируют M заявок, стационарная вероятность состояния любого узла в момент поступления в него новой заявки совпадает со стационарной вероятностью того же состояния рассматриваемого узла в сети, в которой циркулирует на одну заявку меньше, то есть (M − 1) заявок. Это означает, что в сети с M заявками среднее число заявок m_i(M), находящихся в узле i в момент поступления в этот узел новой заявки, равно m_i(M − 1). Тогда среднее время пребывания в узле i поступившей заявки будет складываться из среднего времени обслуживания всех m_i(M − 1) ранее поступивших и находящихся в узле i заявок и средней длительности обслуживания рассматриваемой заявки: .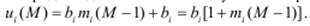

В этом выражении учтено, что среднее время дообслуживания заявки, находящейся в приборе на момент поступления рассматриваемой заявки, равно средней длительности обслуживания b_i в силу свойства отсутствия последействия, присущего экспоненциальному закону. Среднее время пребывания заявки в узле i за время ее нахождения в сети, учитывающее число попаданий α i заявки в данный узел, равно U_i (M) = α _iu_i (M).

Выражения (4.19) и (4.20) представляют собой формулы Литтла для сети, а выражение (4.21) – для узла i, где λ _i(M) = α _iλ ₀(M) – интенсивность потока заявок в узел i (i =1, …, n).

На основе рекуррентных соотношений (4.18) – (4.21) последовательно для M =1, 2, …, M *, где M * – заданное число заявок в замкнутой сети, могут быть рассчитаны средние значения характеристик замкнутой экспоненциальной СеМО.

Заметим, что приведенный метод расчета является точным для замкнутых экспоненциальных СеМО с одноканальными узлами.

Пример 4.4. Рассчитаем характеристики замкнутой однородной экспоненциальной СеМО, полученной путём преобразования разомкнутой СеМО (рис. 4.12), рассмотренной в Примере 4.2, в замкнутую. Положим, что «нулевая точка», отображающая завершение обслуживания заявок в сети и мгновенное формирование новой заявки, выбрана на дуге, выходящей из узла 1 и входящей снова в этот же узел (рис.4.14).

Напомним, что в ЗСеМО относительно «нулевой точки» рассчитываются временные сетевые характеристики: время нахождения в состоянии ожидания и время пребывания заявок в сети, а также производительность ЗСеМО.

ЗСеМО содержит n = 4 одноканальных узла, связи между которыми описываются той же матрицей вероятностей передач:

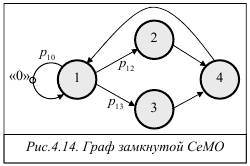
Следовательно, коэффициенты передач для всех узлов, рассчитываемые путём решения системы линейных алгебраических уравнений (4.17), будут иметь те же самые значения: α ₁ =10; α ₂ = 2; α ₃ = 7; α ₄ = 9.

В ЗСеМО циркулирует М заявок, средние длительности обслуживания которых в узлах равны: b₁ = 0, 8с; b₂ = 2с; b₃ = 0, 4 с; b₄ = 0, 3с.

Ниже в табл.4.6 представлены значения времени пребывания u_i(M) и числа заявок m_i(M) в узлах сети, а также среднего времени пребывания U(M) заявок в сети и производительности λ ₀(M), рассчитанные на основе выражений (4.18) – (4.21), для числа циркулирующих в сети заявок M= 1, 2, …, 6. Корректность выполненных расчетов подтверждается тем, что для всех M = 1, 2, …, 6 выполняется проверочное условие:

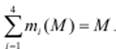
Таблица 4.6

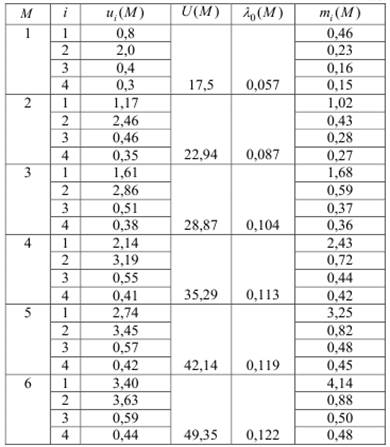
На рис.4.15 представлены зависимости производительности рассматриваемой замкнутой СеМО и среднего времени пребывания заявок в сети от количества M =1, 10 циркулирующих заявок. Анализ полученных результатов показывает, что все характеристики, включая производительность λ ₀ , растут с увеличением M.

Производительность сети асимптотически приближается к максимально возможной производительности (пропускной способности ЗСеМО), совпадающей с предельно допустимой интенсивностью поступления заявок в аналогичной разомкнутой СеМО (см. Пример 4.1), при которой в сети отсутствуют перегрузки, и равна λ ₀ = 0, 125 с^{− 1}.

Среднее время пребывания заявок в ЗСеМО растёт неограниченно с увеличением количества заявок с сети.

Остальные характеристики замкнутой СеМО (загрузки и коэффициенты простоя узлов, время ожидания, длины очередей и число заявок в узлах сети, полное время ожидания в сети) могут быть рассчитаны с использованием фундаментальных соотношений, представленных в разделе 3 (п.3.4.3).

ВЫВОД

Расчёт характеристик функционирования линейных замкнутых однородных экспоненциальных СеМО с одноканальными узлами базируется на так называемой «теореме о прибытии» и проводится с использованием метода средних значений.

АНАЛИЗ СВОЙСТВ ЗАМКНУТЫХ СеМО - 30 мин

Для замкнутых СеМО, как и для разомкнутых, наибольший интерес представляют свойства сети в целом, в частности, влияние циркулирующих в ЗСеМО числа заявок, на такие сетевые характеристики как производительность λ ₀ замкнутой СеМО и среднее время пребывания U заявок в сети.

Анализ представленных на рис.4.16, зависимостей позволяет сформулировать следующие выводы.

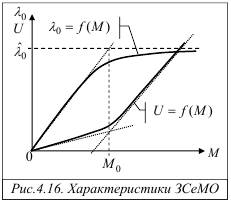1. Зависимость λ ₀ = f (M) производительности ЗСеМО λ ₀ от числа M циркулирующих заявок вначале растёт с увеличением M до некоторого значения M₀, после которого рост производительности замедляется, а с дальнейшим увеличением M производительность сети асимптотически стремится к некоторому предельному значению 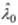, представляющему собой пропускную способность ЗСеМО. Для объяснения этой зависимости вспомним, что производительность замкнутой сети измеряется как интенсивность потока заявок, проходящих через некоторую условную точку, обозначаемую как «0» и расположенную на одной из дуг СеМО, отображающей завершение обслуживания заявок в сети и мгновенное формирование новой заявки, поступающей в сеть. Выше (см. пример 4.4) было показано, что увеличение числа заявок в замкнутой СеМО приводит к увеличению значений всех сетевых характеристик, включая производительность λ ₀. В свою очередь, увеличение производительности приводит к увеличению загрузок узлов СеМО, связанных с интенсивностью λ ₀ зависимостью: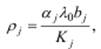

где α _j, b_j и K_j – соответственно коэффициент передачи, средняя длительность обслуживания и количество приборов в узле j =1, n.

Когда число заявок в ЗСеМО достигает некоторого значения M₀, загрузка одного из узлов становится близкой к 1, при этом практически прекращается рост производительности, которая при M → ∞ достигает своего предельного значения – пропускной способности 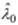. Такой узел представляет собой «узкое место» сети, и значение пропускной способности 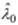определяется пропускной способностью узкого места из условия, что загрузка ρ _у этого узла равна 1:

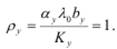
Отсюда пропускная способность замкнутой СеМО:

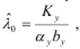
где α _у, b_у и K_у – соответственно коэффициент передачи, средняя длительность обслуживания и количество обслуживающих приборов в узле, являющимся узким местом.

Правая часть последнего выражения представляет собой пропускную способность узла, являющегося узким местом сети: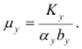

Действительно, α _уb_у представляет собой полное время обслуживания одной заявки в данном узле с учётом того, что заявка за время нахождения в сети в среднем α _у раз побывает в данном узле. Тогда величина, обратная α _уb_у, представляет собой интенсивность обслуживания заявок одним прибором в данном узле: µ₁ =1/α _уb_у, а µ_у = K_уµ₁ – интенсивность обслуживания заявок узлом, то есть всеми приборами.

Этот же результат можно получить следующими рассуждениями.

Если загрузка некоторого узла, являющегося узким местом СеМО, становится равной 1, то это означает, что все приборы данного узла постоянно обслуживают заявки, то есть не простаивают. Тогда интенсивность выходящего из этого узла потока заявок будет равна интенсивности обслуживания: λ _у = µ_у = K_уµ₁. Напомним, что интенсивность потока заявок в узле λ _у связана с производительностью ЗСеМО λ ₀ зависимостью λ _у = α _уλ ₀. Отсюда вытекает, что производительность ЗСеМО равна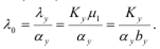

2. Среднее время пребывания заявок (рис.4.16) в замкнутой СеМО, как и производительность, растёт с увеличением числа M циркулирующих в сети заявок, причём вначале наблюдается незначительный рост, а затем, после значения M = M₀, наблюдается линейный рост времени пребывания.

Действительно, если в сети циркулирует только одна заявка, то в такой сети не может быть очередей, и время пребывания заявок в СеМО складывается только из времён обслуживания заявок в узлах с учётом коэффициентов передач:

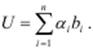
С увеличением числа заявок M в узлах ЗСеМО появляются очереди, причём очевидно, что чем больше заявок в сети, тем более длинные очереди образуются в узлах и тем больше время ожидания, а, следовательно, и время пребывания заявок в ЗСеМО.

Сопоставляя зависимости производительности и среднего времени пребывания заявок от их числа в ЗСеМО, можно сделать следующий вывод: увеличение числа заявок в сети, с одной стороны, приводит к увеличению производительности, что может рассматриваться как положительный фактор, а, с другой стороны, – к увеличению времени пребывания заявок в сети, что является нежелательным фактором.

Точка M = M₀ характеризует некоторое граничное значение числа заявок в ЗСеМО. Дальнейшее увеличение числа заявок в сети оказывается нецелесообразным, поскольку приводит к резкому увеличению времени пребывания заявок в ЗСеМО при незначительном увеличении производительности сети.

3. Когда загрузка узкого места становится равной единице, дальнейший рост производительности за счёт увеличения числа заявок в ЗСеМО невозможен. Для увеличения производительности ЗСеМО, как и в РСеМО, необходимо разгрузить узкое место, то есть уменьшить загрузку: 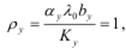что при одной и той же производительности может быть достигнуто:

• уменьшением длительности обслуживания заявок b_у, например за счет увеличения скорости работы (быстродействия) обслуживающего прибора;

• увеличением числа обслуживающих приборов K_у в узле;

• уменьшением коэффициента передачи α _у или, что то же самое, вероятности передачи заявок к узлу, являющемуся узким местом.

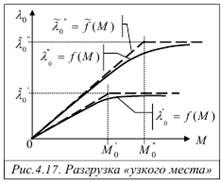Если до разгрузки узкого места зависимость производительности ЗСеМО от числа заявок в сети имела вид λ '₀= f(M) (рис.4.17), а пропускная способность была равна , то после разгрузки – зависимость производительности от числа заявок будет иметь вид λ " ₀ = f(M), а пропускная способность станет равной 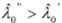. При этом граничное значение числа заявок в ЗСеМО увеличится: M" ₀> M'₀

Следует отметить, что к рассматриваемой зависимости производительности ЗСеМО λ ₀ от числа M циркулирующих в сети заявок может быть применена линейная аппроксимация 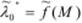, показанная на рис.4.17 в виде пунктирных линий и представляющая собой верхнюю границу производительности ЗСеМО. Последнее означает, что производительность ЗСеМО будет не больше, чем рассчитанное верхнее значение.

Нетрудно представить себе и изобразить на графике, как изменится зависимость среднего времени пребывания заявок в замкнутой СеМО от числа циркулирующих в сети заявок после разгрузки узкого места.

Отметим, что в некоторых случаях разгрузка узкого места не приводит к улучшению характеристик СеМО, в частности, к увеличению производительности. Обычно это связано с тем, что в СеМО может существовать несколько узлов, являющихся «узкими местами». Условием этого является равенство загрузок узлов: ρ _i = ρ _j или 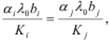откуда окончательно получим: 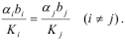В этом случае для улучшения характеристик ЗСеМО необходимо одновременно разгрузить все «узкие места».

Последовательно разгружая узкие места СеМО, мы можем прийти к некоторой «идеальной» сети, в которой загрузки всех узлов одинаковы.

СеМО, в которой загрузки всех узлов равны, называется сбалансированной. Сбалансированная СеМО обладает наилучшими характеристиками по сравнению с несбалансированной.

При построении реальных систем, моделями которых служат СеМО, необходимо, по-возможности, строить сбалансированные системы, хотя на практике по многим причинам достичь этого не удаётся.

ВЫВОД