
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ряды ФРП. Область сходимости.
|
|
Сходимость степенного ряда.
Интервал сходимости, радиус сходимости и область сходимости
Не нужно пугаться такого обилия терминов, они идут «рядом друг с другом» и не представляют особых сложностей для понимания. Лучше выберем какой-нибудь простой подопытный ряд и сразу начнём разбираться.
Прошу любить и жаловать степенной ряд 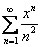 .
.
Переменная 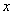 может принимать любое действительное значение от «минус бесконечности» до «плюс бесконечности». Подставим в общий член ряда несколько произвольных значений «икс»:
может принимать любое действительное значение от «минус бесконечности» до «плюс бесконечности». Подставим в общий член ряда несколько произвольных значений «икс»:
Если 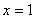 , то
, то 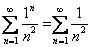
Если 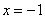 , то
, то 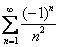
Если 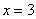 , то
, то 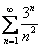
Если 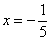 , то
, то 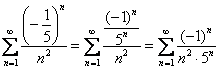
И так далее.
Очевидно, что, подставляя в 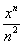 то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной ряд
то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной ряд 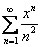 будетсходиться. Такое множество и называется областью сходимости ряда.
будетсходиться. Такое множество и называется областью сходимости ряда.
Для любого степенного ряда (временно отвлекаемся от конкретного примера) возможны три случая:
1) Степенной ряд сходится абсолютно на некотором интервале 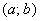 . Иными словами, если мы выбираем любое значение «икс» из интервала
. Иными словами, если мы выбираем любое значение «икс» из интервала 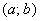 и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал
и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал 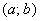 и называется интервалом сходимости степенного ряда.
и называется интервалом сходимости степенного ряда.
Радиус сходимости, если совсем просто, это половина длины интервала сходимости:
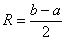
Геометрически ситуация выглядит так:
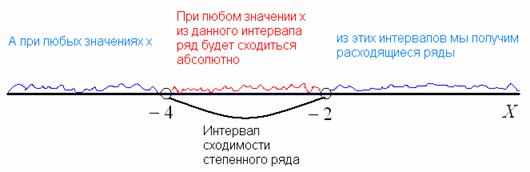
В данном случае, интервал сходимости ряда: 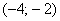 , радиус сходимости ряда:
, радиус сходимости ряда: 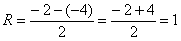
Широко распространен тривиальный случай, когда интервал сходимости симметричен относительно нуля:
 >
>
Здесь интервал сходимости ряда: 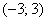 , радиус сходимости ряда:
, радиус сходимости ряда: 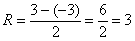
А что будет происходить на концах интервала  ? В точках
? В точках  ,
,  степенной рядможет, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
степенной рядможет, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
– Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости: 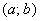
– Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости ряда представляет собой полуинтервал:  или
или 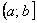 .
.
– Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок: 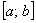
Термины очень похожи, область сходимости ряда – это чуть более детализированныйинтервал сходимости ряда.
С двумя оставшимися случаями всё короче и проще:
2) Степенной ряд сходится абсолютно при любом значении 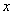 . То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают:
. То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: 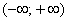 . Радиус сходимости:
. Радиус сходимости: 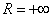 . Рисунок приводить не буду, думаю, нет необходимости.
. Рисунок приводить не буду, думаю, нет необходимости.
3) Степенной ряд сходится в единственной точке. Если ряд имеет вид 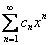 , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке 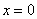 . В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:
. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю: 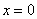 . Если ряд имеет вид
. Если ряд имеет вид 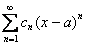 , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке 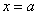 , если ряд имеет вид
, если ряд имеет вид 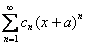 , то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой:
, то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой: 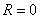 .
.
Других вариантов нет. Область сходимости степенного ряда – это всегда либо единственная точка, либо любое «икс», либо интервал 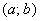 (возможно полуинтервал, отрезок). Подчеркиваю, что данная классификация справедлива для степенных рядов. Для произвольного функционального ряда она в общем случае является неверной.
(возможно полуинтервал, отрезок). Подчеркиваю, что данная классификация справедлива для степенных рядов. Для произвольного функционального ряда она в общем случае является неверной.
|
|
