
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Производная ФКП. Условия Коши-Римана. Аналитические функции.
|
|
Понятие функции комплексной переменной
Сначала освежим знания о школьной функции одной переменной:
Функция одной переменной 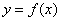 – это правило, по которому каждому значению независимой переменной
– это правило, по которому каждому значению независимой переменной 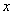 (из области определения) соответствует одно и только одно значение функции
(из области определения) соответствует одно и только одно значение функции 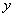 . Естественно, «икс» и «игрек» – действительные числа.
. Естественно, «икс» и «игрек» – действительные числа.
В комплексном случае функциональная зависимость задается аналогично:
Однозначная функция комплексной переменной 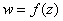 – это правило, по которому каждому комплексному значению независимой переменной
– это правило, по которому каждому комплексному значению независимой переменной 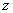 (из области определения) соответствует одно и только одно комплексное значение функции
(из области определения) соответствует одно и только одно комплексное значение функции 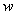 . В теории рассматриваются также многозначные и некоторые другие типы функций, но для простоты я остановлюсь на одном определении.
. В теории рассматриваются также многозначные и некоторые другие типы функций, но для простоты я остановлюсь на одном определении.
Чем отличается функция комплексной переменной?
Главное отличие: числа комплексные. Я не иронизирую. От таких вопросов нередко впадают в ступор, в конце статьи историю прикольную расскажу. На уроке Комплексные числа для чайников мы рассматривали комплексное число в виде 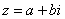 . Поскольку сейчас буква «зет» стала переменной, то её мы будем обозначать следующим образом:
. Поскольку сейчас буква «зет» стала переменной, то её мы будем обозначать следующим образом: 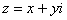 , при этом «икс» и «игрек» могут принимать различные действительныезначения. Грубо говоря, функция комплексной переменной
, при этом «икс» и «игрек» могут принимать различные действительныезначения. Грубо говоря, функция комплексной переменной 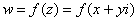 зависит от переменных
зависит от переменных 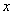 и
и 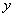 , которые принимают «обычные» значения. Из данного факта логично вытекает следующий пункт:
, которые принимают «обычные» значения. Из данного факта логично вытекает следующий пункт:
Действительная и мнимая часть функции комплексной переменной
Функцию комплексной переменной можно записать в виде:
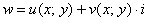 , где
, где 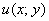 и
и 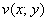 – две функции двух действительных переменных.
– две функции двух действительных переменных.
Функция 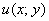 называется действительной частью функции
называется действительной частью функции 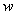 .
.
Функция 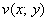 называется мнимой частью функции
называется мнимой частью функции 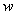 .
.
То есть, функция комплексной переменной 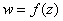 зависит от двух действительных функций
зависит от двух действительных функций 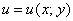 и
и 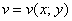 . Чтобы окончательно всё прояснить рассмотрим практические примеры:
. Чтобы окончательно всё прояснить рассмотрим практические примеры:
Пример 1
Найти действительную и мнимую часть функции 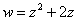
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Решение: Независимая переменная «зет», как вы помните, записывается в виде 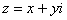 , поэтому:
, поэтому:
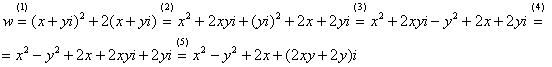
(1) В исходную функцию 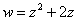 подставили
подставили 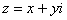 .
.
(2) Для первого слагаемого использовали формулу сокращенного умножения 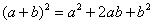 . В слагаемом
. В слагаемом 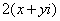 – раскрыли скобки.
– раскрыли скобки.
(3) Аккуратно возвели в квадрат 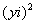 , не забывая, что
, не забывая, что 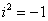
(4) Перегруппировка слагаемых: сначала переписываем слагаемые, в которых нет мнимой единицы (первая группа), затем слагаемые, где есть 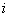 (вторая группа). Следует отметить, что перетасовывать слагаемые не обязательно, и данный этап можно пропустить (фактически выполнив его устно).
(вторая группа). Следует отметить, что перетасовывать слагаемые не обязательно, и данный этап можно пропустить (фактически выполнив его устно).
(5) У второй группы выносим 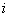 за скобки.
за скобки.
В результате наша функция оказалась представлена в виде 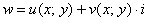
Ответ:
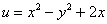 – действительная часть функции
– действительная часть функции 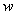 .
.
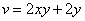 – мнимая часть функции
– мнимая часть функции 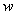 .
.
Что это получились за функции? Самые что ни на есть обыкновенные функции двух переменных, от которых можно найти такие популярные частные производные. Без пощады – находить будем. Но чуть позже.
Кратко алгоритм прорешанной задачи можно записать так: в исходную функцию подставляем 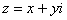 , проводим упрощения и делим все слагаемые на две группы – без мнимой единицы (действительная часть) и с мнимой единицей (мнимая часть).
, проводим упрощения и делим все слагаемые на две группы – без мнимой единицы (действительная часть) и с мнимой единицей (мнимая часть).
Пример 2
Найти действительную и мнимую часть функции 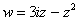
Это пример для самостоятельного решения. Перед тем как с шашками наголо броситься в бой на комплексной плоскости, позвольте дать самый важный совет по теме:
БУДЬТЕ ВНИМАТЕЛЬНЫ! Внимательным нужно быть, конечно, везде, но в комплексных числах следует быть внимательным, как никогда! Помните, что 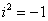 , аккуратно раскрывайте скобки, ничего не теряйте. По моим наблюдениям, самой распространенной ошибкой является потеря знака. Не спешите!
, аккуратно раскрывайте скобки, ничего не теряйте. По моим наблюдениям, самой распространенной ошибкой является потеря знака. Не спешите!
Полное решение и ответ в конце урока.
Чтобы дальше легче жилось, обратим внимание на пару полезных формул. В Примере 1 было выяснено, что 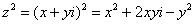 .
.
Теперь куб. Используя формулу сокращенного умножения 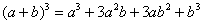 , выведем:
, выведем:
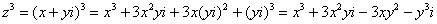 .
.
Рекомендую переписать в тетрадь две рабочие формулы:
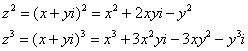
Формулы очень удобно использовать на практике, поскольку они значительно ускоряют процесс решения.
Дифференцирование функций комплексной переменной.
Условия Коши-Римана
У меня есть две новости: хорошая и плохая. Начну с хорошей. Для функции комплексной переменной 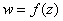 справедливы правила дифференцирования и таблица производных элементарных функций. Таким образом, производная берётся точно так же, как и в случае функции действительной переменной
справедливы правила дифференцирования и таблица производных элементарных функций. Таким образом, производная берётся точно так же, как и в случае функции действительной переменной 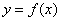 .
.
Плохая новость состоит в том, что для многих функций комплексной переменной производной не существует вообще, и приходится выяснять, дифференцируема ли та или иная функция. А «выяснять», как чует ваше сердце, связано с дополнительными заморочками.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Рассмотрим функцию комплексной переменной 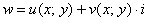 . Для того, чтобы данная функция была дифференцируема необходимо и достаточно:
. Для того, чтобы данная функция была дифференцируема необходимо и достаточно:
1) Чтобы существовали частные производные первого порядка 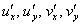 . Об этих обозначениях сразу забудьте, поскольку в теории функции комплексного переменного традиционно используется другой вариант записи:
. Об этих обозначениях сразу забудьте, поскольку в теории функции комплексного переменного традиционно используется другой вариант записи: 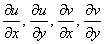 .
.
2) Чтобы выполнялись так называемые условия Коши-Римана:
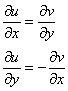
Только в этом случае будет существовать производная!
Пример 3
Определить действительную 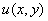 и мнимую
и мнимую 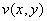 части функции
части функции 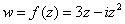 . Проверить выполнение условий Коши-Римана. В случае выполнения условий Коши-Римана, найти производную функции.
. Проверить выполнение условий Коши-Римана. В случае выполнения условий Коши-Римана, найти производную функции.
Решение раскладывается на три последовательных этапа:
1) Найдём действительную и мнимую часть функции. Данное задание было разобрано в предыдущих примерах, поэтому запишу без комментариев:
Так как 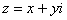 , то:
, то:
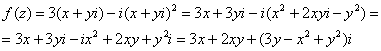
Таким образом:
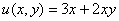 – действительная часть функции
– действительная часть функции 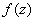 ;
;
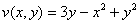 – мнимая часть функции
– мнимая часть функции 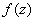 .
.
Остановлюсь еще на одном техническом моменте: в каком порядке записывать слагаемые в действительной и мнимой частях? Да, в принципе, без разницы. Например, действительную часть можно записать так: 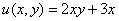 , а мнимую – так:
, а мнимую – так: 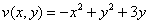 .
.
3) Проверим выполнение условий Коши Римана. Их два.
Начнем с проверки условия 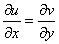 . Находим частные производные:
. Находим частные производные:
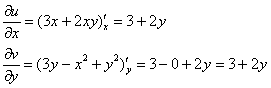
Таким образом, условие 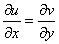 выполнено.
выполнено.
Несомненно, приятная новость – частные производные почти всегда очень простые.
Проверяем выполнение второго условия 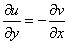 :
:
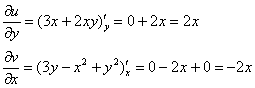
Получилось одно и то же, но с противоположными знаками, то есть, условие 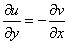 также выполнено.
также выполнено.
Условия Коши-Римана выполнены, следовательно, функция дифференцируема.
3) Найдём производную функции. Производная тоже очень простая и находится по обычным правилам:
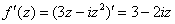
Мнимая единица при дифференцировании считается константой.
Ответ: 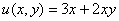 – действительная часть,
– действительная часть, 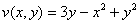 – мнимая часть.
– мнимая часть.
Условия Коши-Римана выполнены,  .
.
|
|
