Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Интеграл ФКП. Теорема Коши.

Теорема Коши позволяет также установить связь между значениями аналитической функции 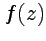во внутренних точках области ее определения и граничными значениями. При этом имеет место следующее соотношение (рис.19):
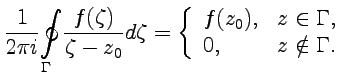
	(52)
Рис.19

Формула (52) называется интегральной формулой Коши или интегралом Коши. Если в качестве контура 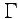в (52) выбрать окружность 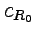, то, заменяя 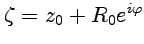и учитывая, что 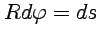- дифференциал длины дуги 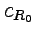, интеграл Коши можно представить в виде формулы среднего значения:

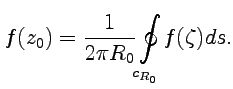
(53)

Формула Коши может быть расширена для производных аналитической функции 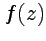, и так как 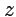входит в интеграл (52) как параметр, то на основе свойств интегралов, зависящих от параметра, после 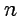-кратного дифференцирования, можно получить

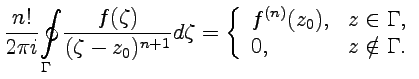
(54)

Помимо самостоятельного значения интегральной формулы Коши, (52), (54) фактически дают очень удобный способ вычисления контурных интегралов, которые, как видно, будут выражаться через значение " остатка" подынтегральной функции в точке, где эта функция имеет особенность .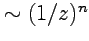

Пример 3-9. Вычислить интеграл от функции 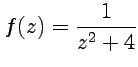по контуру 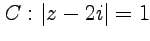(рис.20).

Решение. Точка 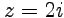, в которой функция 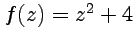имеет особенность, в отличие от примера 4-1, находится внутри окружности 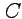. Представим интеграл в форме (52):
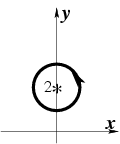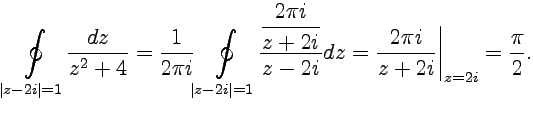