Осциляторів.

Процес зміни в часі параметрів технічного об'єкту (ТО) з багатократним чергуванням їх зростання і убування прийнято називати коливаннями. При колива­ннях відбувається знакозмінне відхилення параметрів від їх певних значень. Ці значення можуть відповідати сталому стану ТО або ж, у свою чергу, змінюватися в часі по деякому закону. Як правило, ко­ливання супроводжує перетворення однієї форми енергії в іншу.

У широкому сенсі під осцилятором (від латинського слова oscillo — гойдаюся) розуміють будь-яку систему, певні параметри якої здійснюють коливання за відсутності змінних зовнішніх дій. У такій системі колива­ння можуть мати різну фізичну природу. Одним з простих осциляторів, в якому можна збудити елек­тромагнітні коливання, є коливальний контур, що складається з електричного конденсатора і індуктивної котушки (рис. 10.1), і мають єм­ність С і

і індуктивність L відповідно. За певних умов електромагнітні коливання можливі в ланцюгах, що містять, о­крім конденсаторів, і котушок також і резистори (див. рис. 9.1, а і б, рис. 9.4, лекція 9).

Рис.10.1

Добре відомим прикладом осцилятора в механічній системі є тіло масою m, приєднане до нерухомої опори за допомогою пружного елементу (пружини) жорсткі­стю с (див. рис. 9.2, лекція 9). Враховуючи, що швидкість v тіла пов'язана з його переміщенням і відносно положення рівноваги співвідношенням v = du/dt, запишемо (9.7), (лекція 9) у вигляді лінійного ЗДР другого порядку

+ cu (t) =P* (t), (10.13)

де — коефіцієнт тертя при русі тіла по горизон­тальній площині, S — площа поверхні контакту тіла з цією площиною, P* (t) — зовнішня сила,

прикладена до тіла і залежна (у загальному випадку) від часу t.

Якщо P (t) = 0 і у момент часу t = 0 відомі значення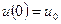

І , то за умови 0 = 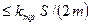= 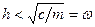ЗДР (10.13) має

Рис. 10.2

рішення [1]

u (t)= 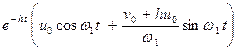, (10.14)

де . Вираз у скобках можна також пред­ставити у вигляді 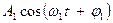, где

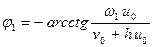, . (10.15)

Через проміжки часу , не залежні від початкових умов і ,, тіло проходе положення рівноваги и = 0, а через проміжки 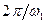функція u (t) досягає максималь­них (або мінімальних) значень (рис. 10.2), які відповідають моментам перетворення на нуль швидкості

.

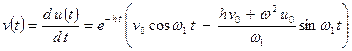Кожне максимальне за абсолютним значенням відхилення від положення рівноваги називають напіврозмахом коливань [1].

З (10.15) витікає, що з часом напіврозмахи коливань зменшуються, причому відношення двох послідовних напіврозмахів в одну і ту ж сторону від положення рівноваги постійно і дорівнює > 1. Натуральний логарифм 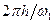цього відношення носить назву логарифмічного декремента коливань (від латинського слова decrementum — зменшення, спад). Таким чином, математична модель, що включає ЗДР (10.13), описує затухаючі коливання, напіврозмахи яких утворюють геометричну прогресію. Через лінійність цього ЗДР відповідний осцилятор прийнято називати лінійним осцилятором.

Якщо нехтувати опором руху тіла у гори­зонтальній площині (див. рис. 9.2, лекція 9), то, вважаючи в (10.13) —(10.15) h = 0, отримуємо ЗДР

+ cu (t) = 0(10.16)

і його рішення

, (10.17)

де 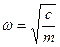— кутова (звана інколи круговою або циклічною) частота цих коливань, що не залежна від початкових умов і визначає період

Т = 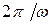коливань, вимірюваний в с, А — амплітуда коливань,

а 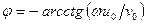. В цьому випадку осцилятор називають гармонійним осцилятором. Відзначимо, що на відміну від кутової частоти, вимірюваної в рад/с, частоту коливань 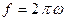вимірюють в герцах (Гц).

На відміну від гармонійних, затухаючі коливання не є, строго кажучи, періодичним процесом, але зберігають деякі його властивості, зокрема чергування через рів­ні проміжки часу 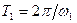максимумів і мінімумів величини u (t). Тому 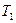прийнято називати умовним пе­ріодом затухаючих коливань, — їх умовною кутовою частотою, а напіврозмахи коливань — їх умовною амплітудою.

Якщо в (9.2) (лекція 9) покласти R = 0 і 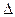U *(t) = 0, то після дифе­ренціювання за часом отримаємо ЗДР другого порядку

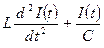= 0, (10.18)

де I (t) — сила струму в коливальному контурі, зображеному на рис. 10.1, а L і С — індуктивність котушки і ємність конденсатора відповідно. Аналогічне ЗДР

, (10.23)

що описує гармонійні коливання в цьому контурі падіння напруги 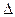U на конденсаторі або котушці, виходить з (9.4) (лекція 9) при 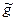= 0 і 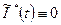. Період коливань сили струму і падіння напруги в цьому контурі рівний .

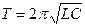Незалежно від фізичного вмісту процесу коливань кожне з ЗДР (10.16), (10.18) і (10.19) називають рівнянням гармонійного осцилятора. Приведемо енергетичне трактування цих ЗДР. Використовуючи рівність 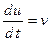, представимо (10.16) у вигляді

= = = ,

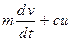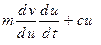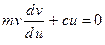або d (mv ²/2)+ d (cu ²/2) = 0. Враховуючи значення і у момент часу

t = 0, після інтеграції знаходимо

, (10.20)

тобто повна енергія W даної механічної системи, рівна сумі кінетичної енергії К = mv² / 2 тіла і потенційній енергії П = сu²/ 2, запасеною в пружині (див. рис. 9.2, лекція 9), у будь-який момент часу залишається постійною. Систему, в якій повна енергія не змінюється в часі, називають консервативною (від латинського слова conservo — зберігаю).