Тоді можна записати

;

.

Для лінійної системи

. (10.1)

Рівняння (10.1) описує принцип суперпозиції: суперпози­ція індивідуальних збурюючих дій наводить до реак­ції, яка є суперпозицією індивідуальних реакцій.

Характерною властивістю лінійної системи є допусти­мість принципу суперпозиції.

Наслідком принципу суперпозиції є:

1. Відсутність якої-небудь збурюючої дії, впливового на

інші збурюючі дії.

2. Відсутність пересічних реакцій, викликаних різними

збурюючими діями.

3. Поєднання збурюючих дій може бути виявлене по поєднанню реакцій визначенням залежності кожної збурюючої дії від реакції і подальшого об'єднання або накладення реакцій для визначення сумарної реакції си­стеми на сумарну збурюючу дію.

Іншим висновком, який виходить з принципу суперпозиції, є те, що якщо на лінійну систему діє п однако­вих збурюючих впливів, то реакція від такої дії визначиться як п однакових реакцій, кожна з яких є реакцією системи на одну збурюючу дію, тобто

.(10.2)

З (10.2) видно, що лінійні системи зберігають масштабний чинник збурюючої дії при переході від входу до виходу системи. Це властивість лінійних систем називають принципом однорідності.

Якщо співвідношення (10.1) і (10.2) справедливі для лінійних си­стем, то це не означає, що виконання одне або іншого умо­ви досить для визначення властивостей лінійної системи.

Система лінійна тоді і лише тоді, коли задовольняються як (10.1), так і (10.2).

Крім того, лінійна стаціонарна система характеризується її реакцією на періодичну збурюючу дію.

Якщо періодична збурююча дія має часто­ту F, то стаціонарна лінійна система відповість на нього періоди­чною реакцією з частотою F.

Коротше кажучи, реакція стаціонарної лінійної системи володіє тими ж спектральними компонентами, що і збурюючі дії.

Вважають, що лінійна система має бути стаціонарна, якщо

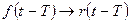, (10.3)

де Т — довільний час запізнювання.

Лінійні системи — це такі системи, динаміка яких моделюється лінійними рівняннями.

Це можуть бути лінійні рівняння алгебри, лінійні диференціальні рівняння, лінійні різницеві рівняння або їх комбінації.

Розглянемо диференціальне рівняння

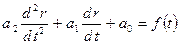, (10.4)

де t — незалежна змінна f (t) - функція збурюючої дії і — реакція.

Коефіцієнти і — система параметрів. Коефіцієн­ти можуть змінюватися або не змінюватися від часу, вони, як пра­вило, повністю визначаються кількістю і типом елементів в системі.

Рівняння (10.4) — просте диференціальне рівняння друго­го порядку. Крім того, рівняння (10.4) є лінійним рівнянням по наступних причинах:

1) ні змінна , ні які-небудь її похідні не містять
ступні більше першого;

2) жоден з його членів не містить добутків два або
більшого числа одних і тих же залежних змінних або добутків залежної змінної на яку-небудь похідну.

Допускаючи принцип суперпозиції, ми приходимо до наступного:

;

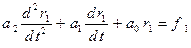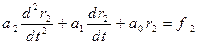
Складаючи ці рівняння, переконуємося, що принцип суперпози­ції виконується:

.

Надалі ми побачимо, що принцип суперпозиції вірний для будь-яких стаціонарних і нестаціонарних процесів.

Будь-яке звичайне диференціальне рівняння 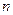-го поряд­ку можна записати як

(10.5)

де коефіцієнти і збурююча дія наведені як функції незалежної змінної t. Говорять, що це рівняння однорід­не, якщо збурююча дія дорівнює нулю, і неоднорідне, якщо збурююча дія відмінна від нуля. Можна записати (10.5) у формі

, (10.6)

якщо позначимо

(10.7)

де L є оператором залежної змінної .

Використовуючи (10.6), можна сформулювати наступні основні властивості лінійних диференціальних рівнянь.

1. Множення залежної змінної на постійний множник рівносильно множенню оператора на ту ж саму константу :

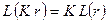. (10.8)

Якщо L (r) = 0 (випадок однорідного рівняння), то

L(Kr)= 0. (10.9)

З цього виходить, що r (t), що є розв’язком однорідного рівняння

L (r) = 0, служить також вирішенням випадку Kr (t).

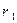2. Заміна на де і 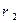лінійно незалежні, призводить
до суми двох лінійних операторів, один від 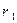, інший від .

У зв'язку з цим зрозуміло, що

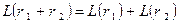(10.10)

і

= 0 лише при . (10. 11)

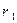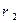Співвідношення (10.10) і (10.11) стверджують, що якщо и є вирішеннями однорідного рівняння L (r)= 0, то тоді і є також його рішенням.

З властивостей 1 і 2 видно також, що якщо 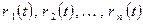— лінійні незалежні вирішення однорідного лінійного диферен­ційного рівняння, то

L (r) = 0, також і для їх лінійних ком­бінацій , коли с — незалежні кон­станти.

3. Рішення з п незалежними константами є загальним вирішенням однорідного диференційного рівняння за
умови, що п частинних рішень 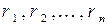лінійно незалежні.­
І, навпаки, рішення мають бути лінійно ­незалежними, якщо жодне з них не може бути виражене через лінійні комбінації інших.

Загальне вирішення однорідного рівняння часто називають додатковою функцією.

4. Якщо r_ч — частинне рішення неоднорідного рівняння при
L (r_ч) 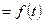, то сума цього частинного рішення і додаткової
функції є повним вирішенням неоднорідного лінійного диференціального рівняння.

Взагалі, будь-яке рішення (10.4) може бути записане як комбінація додаткової функції і частинного рішення (інколи називається приватним інтегралом):

r(t) = r_Д (t) + r_ч(t). (10.12)

Можна відмітити, що якщо 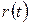- рішення (10.4) і 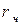- частинне рішення (10.4), то

.

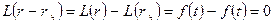Звідси є вирішенням однорідного рівняння, яке через властивості довільної постійної с може бути записано наступним чином

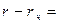
Перенісши частинне рішення цього рівняння управо, отримаємо бажане рішення.

5. Для знаходження чисельних значень п констант потребує знання п значень вирішення рівняння і його похідної. Невідомі коефіцієнти визначають вирішенням системи рівнянь при підстановці чисельних значень реакцій і їх похідних.

Відмітимо, що їх значення можна вибирати у відомі, не обов’язково однакові моменти часу.