Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Проекций и решение метрических

задач

К последовательной замене двух плос-костей проекций следует прибегать при ре-шении вторых основных задач на прямую и плоскость, решаемые способами вращения вокруг проецирующих осей и плоско-парал-лельным перемещением двумя преобразо-ваниями.

Сущность процесса двойного преобра-зования исходных проекций точки А заклю-чается в следующем (рис. 11.28)

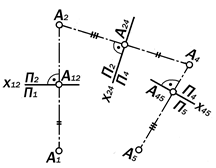
Рис.11.28. Последовательное преобразование проекций точки А двумя заменами плоскостей проекций

Допустим, первой заменим плоскость П₁ на плоскость П₄ ^ П₂, т.е.,

1. х₁₂ ↷ х₂₄; тогда:

2. А₂ А₄ ^ х₂₄ ; А₄ А₂₄ = А₁ А₁₂;

после этого: 3. х₂₄ ↷ х₄₅ и тогда:

4. А₄ А ₅ ^ х₄₅; А ₄₅ А ₅ = А ₂ А ₂₄.

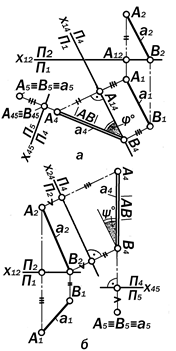
Рис. 11.29. Преобразование проекций

отрезка АВ прямой а общего положе-

ния в его проекции в проецирующем положении

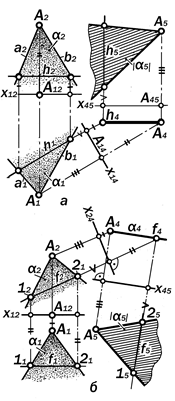
Рис. 11.30. Преобразование проекций

плоскости общего положения в её

проекции в положении уровня

3. Графические решения второй

основной задачи на прямую

Задача 2.1. Преобразовать проекции отрезка АВ прямой а общего положения в проекции этой же прямой, но в проецирую-щем положении (рис.11.29, а, б).

Решение: Так как по условию данный отрезок АВ занимает в пространстве общее положение, то заменённое положение той или иной плоскости проекций, перпендику-лярное к этому отрезку, также будет зани-мать в пространстве общее положение по отношению к незаменённой плоскости ис-ходной системы П₁ ^ П_{2 .} Поэтому, для со-блюдения ортогональности новых положе - ний плоскостей проекций необходимо преж-де решить первую основную задачу на пря-мую (см. рис. 11.26, а, б), а затем, приняв результат её решения за исходное условие, решать данную задачу (рис. 11.29, а, б):

1. х₁₂ ↷ х₁₄ || А₁В₁; А₄В₄ =

=| АВ |;

2. х₁₄ ↷ х₄₅ ^ А₄ В₄ ;

3. А₄ В₄ → А ₅ В ₅ ^ х₄₅;

4. |(А₄₅ º В₄₅), (А ₅ º В₅)| =

= | А₁ А₁₄ |;

А ₅ º В ₅ º а₅ – точка.

4. Графические решения второй основной задачи на плоскость

Задача 2.2 Преобразовать проекции плоскости a (а ´ b ) общего положения в проекции этой же плоскости в положении уровня (рис.11.30, а, б).

Решение: Так как по условию данная плоскость занимает в пространстве общее положение, то новое положение плоскости проекций, параллельное ей, так же будет занимать в пространстве общее положе-ние, которое не будет перпендикулярным к той плоскости их исходной системы, кото-рая не изменяла своего положения. Поэто-му для соблюдения ортогональности новых положений плоскостей проекций необходи-мо прежде решить первую основную задачу на плоскость (см. рис.11.27, а, б), а затем, приняв результат её решения за исходное условие, решить данную задачу (рис11.30 а, б).

Построения не требуют комментариев.

12.5.3. Замена плоскостей проек-ций на безосном комплексном чертеже

Если сравнивать геометрическую модель преобразования двухкартинно-го комплексного чертежа в трёхкартин-ный (рис.11.31, а) и геометрическую си-туацию, требующую решения первой ос-новной задачи на прямую или плоско-сть, то оказывается очевидной их пол-ная проективная эквивалентность. И действительно, в первом случае вспо-могательное проецирование происхо-дит на плоскость П₃, перпендикулярную как к П₁, так и к П₂, а во втором, - либо к П₁, либо к П₂. Последнее обстоятель-ство приводит к изменению формы графического алгоритма преобразова-ния исходных горизонтальной и фрон-тальной проекции точки в её профиль-ную проекцию (рис.11.31, а) на безосном комплексном чертеже, но не её струк-турного содержания (рис.11.31, б, в).

 

 

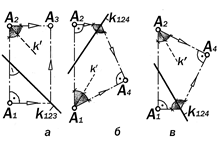
Рис.11.31. Сравнение трёхкартинного комплексного чертежа точки с графической моделью метода замены одной плоскости проекций

 

Обе схемы четырёхзвенны и со-держат пятый графический элемент. В первом случае это постоянная прямая k₁₂₃ трёхкартинного комплексного чер-тежа, расположенная под 45° к верти-кальной линии связи А₁А₂ , во втором случае, - это прямая k₁₂₄, параллельная биссектрисе угла между вертикальной линией связи и направлением проеци-рования на вспомогательную плоскость проекций П₄. (рис.11.31, б, в).

Если проецирование происходит на П₄ ^ П₁, то прямая k₁₂₄ параллельна бис-

сектрисе k¢ между линиями связи А₁А₂ и

А₁ А₄. При этом между А ₁ и А ₄ двух-звенная ломаная линия связи, при А₂

 

 

Рис.11.32. Графическое решение

Сервис онлайн-записи на собственном Telegram-боте

Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.

Для новых пользователей первый месяц бесплатно.

Зарегистрироваться в сервисе

задачи 3.1

 

 

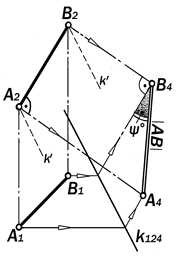
Рис.11.33. Графическое решение задачи 3.2

 

 

перпендикулярная к А₁А₂, а после точ-ки излома на k₁₂₄, - перпендикулярная к линии связи А₁А₄ (рис.12.31, б).

Если проецирование происходит на П₄ ^ П₂, то прямая k₁₂₄ параллельна биссектрисе k¢ между линиями связи А₁А₂ и А₂А₄. При этом между А₁ и А₄ двухзвенная ломаная линия связи, при А₁ перпендикулярная к А₁А₂, а после точки излома на k₁₂₄, - перпендикуляр-ная к линии связи А₂А₄ (рис.12.31, в).

Конструктивным изобразительным свойством полученных графических ал-горитмов является наличие в их струк-туре двух прямых углов.

 

5. Графические решения первой

основной задачи на прямую

Задача 3.1. Преобразовать проекции отрезка АВ прямой а общего положения в её проекции в положении фронтальной ли-нии уровня на чертеже без указания осей (рис.12.32).

Решение: Для того, чтобы на безосном комплексном чертеже преобразовать про-екции отрезка АВ прямой а общего поло-жения в проекции этого же отрезка в поло-жении фронтальной линии уровня, необхо-димо:

1. Через А₁ и В₁ провести линии связи, перпендикулярные к А₁ В₁;

2. Провести биссектрису k¢ между вер-тикальной линией связи А₁А₂ и новым направлением проецирования;

3. Параллельно этой биссектрисе и ис-ходя из композиционных соображений, про-вести прямую k₁₂₄;

4. Через А₂ и В₂ под прямыми углами к

А₁А₂ и В₁В₂ провести горизонтальные линии связи до их пересечения с k₁₂₄;

5. Из полученных точек излома провес-ти вторые участки линий связи до их пере-сечения в искомых вспомогательных проек-циях А₄ и В₄ отрезка АВ, расположившего-ся в пространстве по отношению к не-изображенной плоскости П₄ в положении фронтальной линии уровня.

Проекция А₄В₄ отрезка АВ прямой а об-щего положения содержит в себе непо-средственную информацию о длине этого отрезка и величине угла его наклона к П₁.

Задача 3.2. Преобразовать проекции отрезка АВ прямой а общего положения в её проекции в положении горизонтальнойлинии уровня на чертеже без указания осей (рис.11.33).

Решение этой задачи аналогично ре-шению задачи 3.1.

6. Графические решения второй

основной задачи на прямую

Задача 3.3. Преобразовать проекции отрезка АВ прямой а общего положения в проекции этого же отрезка в проецирую-щем положении на чертеже без указания осей (рис. 11.34).

Решение. Для того, чтобыпроекции от-резка АВ прямой а общего положения пре-образовать в проекции этого же отрезка, находящегося в проецирующем положении, необходимо одну из исходных плоскостей проекций П₁ или П₂ заменить на плоскость П₄, перпендикулярную к этому отрезку. Но, так как отрезок АВ занимает в пространстве общее положение, то и плоскость П₄ по отношению к оставшейся плоскости исход-ной системы также займет общее положе-ние. В итоге возникает позиционная задача на построение точки встречи К отрезка АВ с плоскостью П₄ общего положения, а затем метрическая задача на построение совме-щенного положения П₄ с П₁ вращением её вокруг горизонтального следа (рис11.34 а, б).

Рис.11.34. Преобразование проекций отрезка АВ прямой а общего положения в его проекции в проецирующем положении

а – в осной системе;

б – в безосной системе.

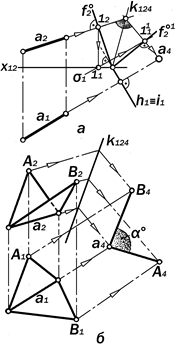
Рис. 11.35. Графическое определение величины двугранного угла при ребре АВ общего положения

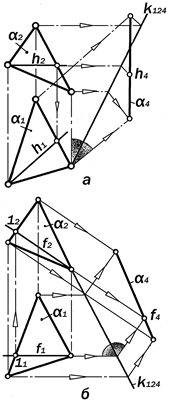
Рис.11.36. Графическое решение задачи 3.4.

В итоге, для решения второй основ-ной задачи на прямую в безосной сис-теме применяется не два, как в осной, а

одно преобразование исходных проек-ций, что более рационально.

При помощи решения второй осно-вной задачи на прямую решаются кон-кретные метрические задачи на опре-ление величины расстояний от точек до прямых общего положения, между па-раллельными и скрещивающимися пря-мыми, а также величин двугранных уг-лов при их произвольно расположен-ных рёбрах (рис11.35, а, б).

7. Графические решения первой

основной задачи на плоскость

Задача 3.4. Преобразоватьпроекции плоскости a (∆ АВС) общего положения в проекции этой же плоскости, находя-щейся в проецирующем положении на чер-теже без указания осей (рис.11.36).

Решение: Для того, чтобы на безосном комплексном чертеже преобразовать прое-кции данной плоскости общего положения в проекции этой же плоскости в проецирую-щем положении достаточно в качестве ос-новного элемента преобразования принять любую её прямую линию и относительно её решить вторую основную задачу на прямую

(см. рис. 11.34.). Эта прямая выродится в точку, а вся плоскость, - в прямую линию.

Если в качестве основного элемента преобразования принять линию уровня плоскости, то графическое решение этой задачи упрощается (рис.11.36, а, б).

а) При главном элементе преобразова-ния, - горизонтали h, необходимо:

= угол между вертикальной линией свя-зи и направлением горизонтальной проек-ции горизонтали разделить на две равные части биссектрисой k¹ , с которой в данном случае совпадает постоянная прямая k₁₂₄ данного трёхкартинного чертежа;

= преобразовать исходные проекции в искомую по схеме графического алгоритма

решения задачи 2.1.

б) При главном элементе преобразова-ния, - фронтали f, необходимо:

= угол между вертикальной линией свя-зи и направлением фронтальной проекции фронтали разделить на две равные части биссектрисой k², с которой в данном слу-чае совпадает постоянная прямая k₁₂₄ дан-ного трёхкартинного комплексного чертежа;

= преобразовать исходные проекции в искомую по алгоритму решения задачи 2.1.

8. Графические решения второй основной задачи на плоскость

Задача 3.5. Преобразовать проекции плос-кости a (∆ АВС) общего положения в проекции этой же плоскости, находящей-ся в положении плоскости уровня на чер-теже без указания осей ( рис.11.37).

Решение: Для того, чтобы проекции плоскости общего положения преобразо-вать в проекции этой же плоскости в поло-жении уровня, необходимо одну из исход-ных плоскостей проекций П₁ или П₂ заме-нить на плоскость П₄, параллельную дан-ной плоскости.

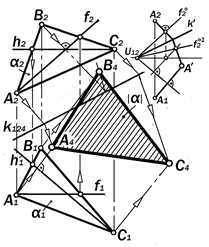
Рис. 11.37. Графическое решение

задачи 3.5

Так как плоскость П₄ параллельна плос-кости a общего положения, то она также занимает в пространстве общее положе-ние. В частности, плоскость П₄ может сов-падать с плоскостью a и поэтому для пос-троения истинного вида треугольника АВС достаточно совместить его плоскость с го-ризонтальной или фронтальной плоскос-тями уровня способом вращения вокруг со-ответствующей линии уровня.

При этом следует предварительно по-строить графический алгоритм искомого преобразования (рис.11.37, а) с участием постоянной прямой k₁₂₄ и решать задачу с использованием этого алгоритма.

Выводы к п. 11.5.3: 1. Перед непосред-ственным графическим решением той или

иной метрической задачи на прямую или плоскость необходимо построить соот-

ветствующий графический алгоритм ис-комого преобразования;

2. В отличие от решения вторых осно-

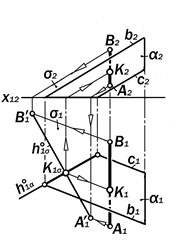
Рис. 11.38. Графическое решение

задачи 4.1.

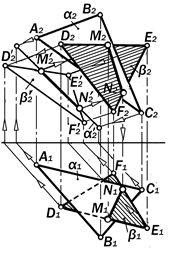
Рис. 11.39.. Графическое решение

задачи 4.2.

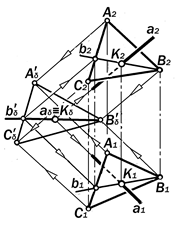
Рис. 11.40. Графическое решение

задачи 4.3.

вных задач на прямую и плоскость в осной системе, решаемых двумя преобразова-ниями, в безосной системе эти задачи ре-шаются одним преобразованием, что бо-лее рационально.