Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Проецирующих осей

Известно, что вращательным во-круг оси і является такое движение точ-ки А, при котором она перемещается по окружности а, плоскость a кривизны ко-торой перпендикулярна к этой оси и пе-

ресекает её в точке О, - центре враще-ния. При этом радиус R этой окружнос-ти равен расстоянию от вращающейся точки А до центра О её вращения (рис. 11. 2).

В случае, когда точка В лежит на оси і, то она совпадает со своим цент-ром вращения, радиус её вращения равен нулю и потому она неподвижна.

Если вокруг одной оси вращается не одна точка, а геометрический объект как система взаимосвязанных точек, то каж-дая из них перемещается в своей плос-кости вращения как плоскости кривизны её траектории движения, радиус которой определяется расстоянием от этой точ-ки до оси і.

Вполне очевидно, что эти плоскос-ти, будучи перпендикулярными к одной

прямой, между собой будут параллель-ны (рис. 11. 3).

Так как в процессе вращения систе-мы точек вокруг одной оси её внутрен-няя метрика не должна нарушаться, то все её точки необходимо поворачивать вокруг этой оси в одну и ту же сторону и на один и тот же угол.

Рационально вращать объект вокруг осей частного положения (проецирую-щих или линий уровня), ибо в этих слу-чаях параллельные между собой пло-скости вращения его точек будут за-

Рис. 11.4. Графическая модель поворота точки А вокруг і ^ П₁ на 120°

Рис. 11. 5. Графическая модель поворота точки В вокруг і ^ П₂ на 360°

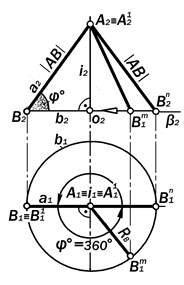
Рис. 11.6. Графическая модель пово-рота отрезка АВ вокруг і ^ П₁ на 360° при А Î і

нимать соответственно положення уро-

вня или проецирующие.

11.2. 1. Способ вращения вокруг одной проецирующей оси и решение метрических задач

1. Вращение точки вокруг і^П₁ и его графическая модель (рис. 11. 4).

Дано і ^ П₁, (і₂ ^ х₁₂; і₁ – точка);

А Ï і; (А₁, А ₂)

Требуется: Повернуть точку А на 120° в положение А¹ вращением вокруг

оси і ^ П₁ против часовой стрелки.

Решение:

1. А Î a ^ і; 3. ОА = R_A;

А₂ Î a₂ ^ і ₂; O₂A₂ = R₂; O₁A₁ = R₁;

2. О = a х і; 4. a - окружность

О₂ = a₂ х і₂; О₁ º і_{1 ;} радиуса R_A.

a₂ º a₂; a₁ º a.

5. A ↷ A¹;

А ₁ ↷ А¹₁ на 120°; А¹₂ = А¹₁ А¹₂ х а₂.

Утверждение 11.1. Если точка А вращается вокруг оси і, перпендику-лярной к П₁, то её горизонтальная проекция перемещается по окружнос-ти а₁ радиуса R_A, равного расстоянию от А₁ до О₁º і₁, а фронтальная про-екция А₂ совершает возвратно-посту-пательное движение по прямой а₂ ^ і₂, максимально удаляясь от і₂ на рассто-яние, равное натуральной величине радиуса R _A вращения точки А.

2. Вращение точки В вокруг і ^ П₂ и его графическая модель (рис. 11.5)

Дано: і ^ П₂ (і₁ ^ П₁; і₂ – точка);

В Ï і; (В₁, В₂ );

Требуется: Повернуть точку В во-круг оси і на 360°.

Решение:

1. В Î b ^ і; 3. ОВ = R_B;

В₁ Î b₁ ^ і₁; O₂B₂ = R₂; O₁B₁ = R₁;

2. О = b х і; 4. b –окружность;

О₁ = b₁ х і₁; О₂ º і₂; радиуса R_B;

b₁ º b₁; b₂ º b;

5. B ↷ B ¹ º B (т.е., на 360°);

Утверждение 11.2. Если точка В вращается вокруг оси і, перпендику-лярной к П₂, то её фронтальная про-екция В₂ перемещается по окружнос-ти b₂ радиуса R_B, равного расстоянию от В₂ до О₂º і₂, а горизонтальная про - екция В₁ совершает возвратно-посту-пательное движение по прямой b₁ ^ i₁,

максимально удаляясь от і₁ на рассто-

яние, равное натуральной величине радиуса R_B вращения точки В.

3. Вращение отрезка АВ прямой а вокруг і ^ П₁ при А Î і и его графичес-кая модель (рис.11.6).

Дано: і ^ П₁ (і₂ ^ х₁₂ ; і₁ - точка).

АВ х і = А; (А₁В₁ ; А₂В₂);

Требуется: Повернуть отрезок АВ вокруг оси і ^ П₁ на 360° против часо-вой стрелки.

Решение:

1. В Î b ^ і; 3. ВО_В = R_B;

В₂ Î b₂ ^ і₂; B₁O₁ = R₁; B₂O₂ = R₂;

2. О_В = b х і; 4. A Î i Þ R_A = 0;

О₂ = b₂ х і₂; О₁ º А₁ º і_1;

5. AB ↷ A¹B¹ º AB, т.е., на 360°.

Утверждение 11.3. Если конец А отрезка АВ прямой а принадлежит оси і ^ П₁ , то, вращаясь вокруг неё, этот отрезок образует коническую поверх -ность Ф с вершиной в точке А и осно-ванием, -окружностью b радиуса R_В, равного расстоянию от точки В до оси і.

Утверждение 11.4. Если ось вра-щения і ^ П₁ и проходит через конец А отрезка АВ, то в процессе преобра-зования его проекций внутренняя мет-рика горизонтальной проекции А₁В₁ не изменяется, а внутренняя метрика её фронтальной проекции А₂В₂ изменяет-ся от значения натуральной величины высоты |AO| = A₂O₂ образуемой кони-ческой поверхности Ф (в положении отрезка АВ || П₃) до значения нату-ральной величины |AB| = A₂B₂ самого отрезка АВ в его положении, паралле-льном П₂.

Утверждение 11.5. Если отрезокАВ из общего положения поворачива-ется вокруг оси і ^ П₁ до положения фронтальной линии уровня, то угол j ° наклона её фронтальной проекции А₂В₂ = | AB | к оси х₁₂ равен натуральной величине угла наклона j ° отрезка АВ к плоскости П₁ (см.рис.11.6).

Из последних утверждений выте - кает ПРАВИЛО 1: Для того, чтобы графически определить длину отрезка

АВ прямой линии а общего положения

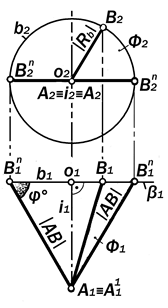
Рис.11.7. Графическая модель поворота отрезка АВ вокруг і ^ П₂ на 360°

при А Î і

Рис.11.8. Графические модели пово-

ротов отрезка АВ вокруг і ^ П₁ (П₂)

при АВ ∸ і.

и угол его наклона П₁ необходимо и до-статочно А₁ совместить с і_1, через

А₂ провести і₂ ^ х₁₂ и А₁В₁, не изменяя

его длины, повернуть до положения А₁ В¹₁ или А₁Вⁿ₁, фронтальная проекция А₂ В¹₂ или А₂Вⁿ₂которого будет содер-жать необходимую метрическую ин-формацию.

4. Вращение отрезка АВ прямой а вокруг і ^ П₂ при А Î і и его графи-

ческая молель (рис. 11.7).

Дано: і ^ П₂ (і₁ ^ х₁₂; і₂ – точка);

а х і = А; (А₁ Î і₁; А₂ º і₂).

Требуется: Повернуть отрезок АВ вокруг оси і на 360° против часовой стрелки.

Решение:

1. В Î b ^ і; 3. ОВ = R_B;

В₁ Î b₁ ^ і₁; B₂O₂ º i₂ º A₂ º

2. О = b х і; º R_2B º | R_B |;

О₁ = b₁ х і₁; О₂ º і₂; 4. A Î і; R_A = 0.

Утверждение 11.6. Если конец А отрезка АВ прямой а общего положе-ния принадлежит оси і ^ П₂, то, вра-щаясь вокруг неё, этот отрезок обра-зует коническую поверхность Ф с вер-шиной в точке А и основанием, - ок-ружностью b радиуса R_B, равного рас-стоянию от точки В до оси і.

Утверждение 11. 7. Если ось враще-ния і ^ П₂ и проходит через конец А отрезка АВ, то в процессе преобра-зования его проекций внутреняя ме-трика её фронтальной проекции А₂В₂ не изменяется, а внутренняя метрика её горизонтальной проекции А₁В¹₁ из-меняется от натуральной величины высоты |AO| = A₂O₂ образуемой кони-ческой поверхности Ф (в положении отрезка АВ || П₃) до натуральной вели-чины |AB| = A₁ B¹₁ = A₁Bⁿ₁ самого отрез-ка АВ в положении, параллельном П₁.

Утверждение 11.8. Если отрезок АВ из общего положения поворачива-ется вокруг оси і ^ П₂ до положения горизонтальной линии уровня, то угол y ° ₁ наклона его горизонтальной про-екции А₁В¹₁ к оси х₁₂ равен натураль-ной величине угла наклона y° отрезка АВ к плоскости П ₂.

Из последних утверждений выте-кает ПРАВИЛО 2: Для того, чтобы графически определить длину отрез-ка АВ прямой а общего положения, и угол его наклона к плоскости П₂ необ-ходимо и достаточно і₂ совместить с А₂, через А₁ провести і₁ ^ х_12, А₂В₂, не изменяя её длины, повернуть до поло-жения А₂В¹₂ или А₂Вⁿ₂, горизонтальные проекции А₁В¹₁ и А₁Вⁿ₁ которых будут содержать необходимую метрическую информацию.

5. Вращение отрезка АВ прямой а вокруг і ^ П₁ (П₂) при і ∸ АВ и его гра-фическая модель ( рис.11.8, а, б).

Дано: і ^ П₁ (П₂); АВ ∸ і.

Требуется: Повернуть отрезок АВ вокруг і ^ П₁ (П₂) на 360° против часо-вой стрелки.

Анализ условия:

Так как отрезок АВ скрещивается с осью і, то все его точки удалены от неё на различные расстояния. Отсюда сле-дует, что на отрезке АВ существует точ-ка С (С₁, С₂), удалённая от оси і на мини-мальное расстояние, измеряемое по перпендикуляру, опущенному из выро-жденной в точку проекции і₁ (і₂) оси і на соответствующую проекцию А₁В₁ (А₂ В₂) отрезка АВ.

Если і ^ П₁ (рис.11.8, а), то С₁О₁ ^ ^ А₁В₁ , С₂О₂ ^ і₂, откуда следует, что С₁О₁ = | R_C |;

Если і ^ П₂, (рис.11.8, б), то С₂О₂ ^

^ А₂В₂ , С₁О₁ ^ і₁ , откуда следует, что С₂О₂ = | R_C |.

Определение 11.1. Радиус вращения точки С отрезка АВ прямой а общего положения, ближайшей к оси вращения і, называется радиусом вращения этой прямой.

Так как все точки отрезка АВ уда-лены от оси і на различные расстояния, то траекториями их вращения будут окружности разных радиусов, плоскости кривизны которых будут плоскостями уровня по отношению к той плоскости проекций, по отношению к которой ось і перпендикурна.

Утверждение 11.9. Если отрезок АВ прямой общего положения, враща-ясь вокруг проецирующей оси, скрещи-вается с нею, то своими последова-тельными положеннями он образует

прямолинейчатый однополостный ги-

-

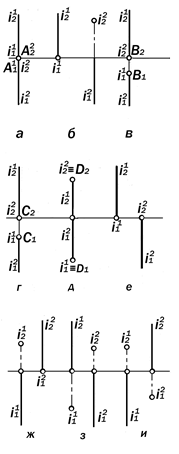
Рис. 11.9. Варианты положения осей последовательного вращения

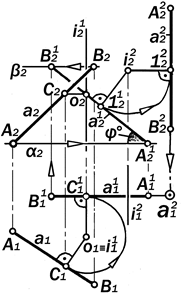
Рис.11.10. Графическая модель

преобразования проекций отрезка АВ общего положення в его проекции проецирующего положення

перболоид вращения, горловиной ко-

торого являеться параллель, образо-ванная вращением точки С, удалённой

от оси і на кратчайшее расстояние.

Утверждение 11.10. Если отрезок АВ вращается вокруг оси і ^ П₁ (П₂), то он дважды проходит через положе-ние, параллельное той плоскости про-екций, по отношению к которой ось вращения параллельна. При этом вну-тренняя метрика вращающейся про-екции отрезка не изменяется, а вну-тренняя метрика проекции, точки ко-торой совершают возвратно-посту-пательные движения, метрически пре-образовываются от величины крат-чайшего расстояния между плоскос-тями вращения его концов А и В (при АВ || П₃) до натуральной величины от-резка АВ (при АВ || П₁ (П₂)).

Из двух последних утверждений следует ПРАВИЛО 3: Для того, чтобы графически определить длину отрез-ка АВ прямой общего положения и угол его наклона к П₁ или к П₂ по его отро-гональным проекциям, необходимо и достаточно расположить ось і ^ П₁ или к П₂, опустить из вырожденной в точку проекции і₁ (і₂ ) оси і перпендику-ляр О₁С₁ = | R_C | на А₁В₁ или О₂С₂=| R_C | на А₂В₂ и повернуть соответствую-щую проекцию О₁С₁ (О₂С₂ ) до положе-ния О₁С¹₁ (С²₁) или О₂С ¹₂ (С ²₂ ), совпа-дающего с вертикальной линией связи.

Тогда А₁В₁ ^ О₁О₁ или А₂В₂ ^ О₂С₂зай - мут положения А¹₁В¹₁ или А¹₂В¹₂, па-раллельное оси проекций х₁₂, а А₂В₂ (А₁В₁) преобразуются в проекции А¹₂В¹₂ или А¹₁В¹₁, содержащие необходимую метрическую информацию (рис.11.8).

Утверждение 11.11. Вращая пря-мую линию общего положения вокруг той или иной проецирующей оси, её можно из общего положения перевес-ти только в положение линии уровня.

Утверждение 11.12. Вращая пря-мую линию уровня вокруг проецирую-щей оси, её можно перевести в поло-жение, перпендикулярное к той плос-кости проекций, по отношению к ко-торой ось вращения параллельна.