Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Способ плоско-параллельно-го перемещения и решение метрических задач

Определение 11. 4. Плоско-параллель-ным называется такое перемещение

объекта в пространстве, при кото-ром все его точки перемещаются во взаимно-параллельных плоскостях без нарушения его внутренней метрики.

В общем случае взаимно-паралле-льные плоскости перемещения точек объекта могут занимать в пространстве общее положение, но для решения кон-кретных метрических задач с их помо-щью их следует принимать в положении плоскостей уровня.

Так как плоскости уровня занимают дважды частное положение, то с их вы-рожденными в горизонтальные прямые линии проекциями, обладающими соби-рательным свойством, совпадут соот-ветствующие проекции траекторий пе-ремещения точек объекта из их началь-ного положения в конечное. При этом

на их невырожденной проекции изобра-жение исходного (общего) и конечного (частного) положения объекта, в силу неизменяемости его внутренней метри-ки, остаются конгруэнтными.

Метрические задачи, решаемые ра-нее методами вращения вокруг проеци-рующих осей и вокруг линий уровня, об-общая, можно разделить на:

1. Основные метрические задачи на прямую:

1.1. проекции прямой общего поло-жения преобразовать в проекции этой же прямой, расположенной в положе-нии линии уровня: а ↷ а¹ || П₁ (П₂);

1.2. проекции прямой общего поло-жения преобразовать в проекции этой же прямой, находящейся в проецирую-щем положении: а ↷ а² ^ П₁ (П₂);

2. Основные метрические задачи на плоскость:

2.1. проекции плоскости общего по-ложения преобразовать в проекции этой же плоскости, находящейся в про-ецирующем положении: a ↷ a¹ ^ П₁ (П₂).

2.2. проекции плоскости общего по-ложения преобразовать в проекции

этой же плоскости, находящейся в по-

ложении уровня: a ↷ a² ^ П₁ (П₂).

Опыт решения этих задач вышерас-смотренными способами показывает, что решения вторых основных задач на прямую и плоскость включают в себя решения первых основных задач, резу-льтаты которых являются для них ис-ходными условиями.

Поэтому рассмотрим графические решения вторых основных задач на прямую и плоскость способом плоско-параллельного перемещения.

Задача № 1.2. Проекцииотрезка АВ прямой а общего положения преобразо-вать в проекции этого же отрезка, нахо-дящегося в проецирующем положении:

а ) АВ ↷ А¹В¹ || П₂ (рис.11.21):

А₁ В₁ ↷ А¹₁ В¹₁ ^ А₁ А₂;

А ₂ В ₂ ® А¹₂ В¹₂ =| АВ | (задача 1.1);

б ) а ↷ а²^ П₁ (рис.11.22):

1. а₁ ↷ а¹₁ ^ А₁ А₂;

а₂ ® а¹₂ = | АВ | (задача 1.1);

2. а¹₂ ↷ а²₂ || А₁ А₂;

а¹₁ ® а²₁ – точка.

При помощи первой и второй основных

задач на прямую линию можно решать сле-дующие конкретные метрические задачи:

1. Определить длину отрезка АВ пря-мой а общего положения и углы его накло- на к плоскостям проекций П₁ и П₂;

2. Определить величину расстояния от точки А до прямой а общего положе-ния;

3. Определить величину расстояния между двумя параллельными прямыми ли-ниями;

4. Определить величину кратчайшего расстояния между двумя скрещивающими-ся прямыми линиями;

5. Определить величину двугранного угла при его ребре.

Решение первой конкретной метрической задачи сводится к первой основной задаче на прямую. Решения 2…5–й конкретных метрических задач сводится к решению вто-

рой основной задачи на прямую.

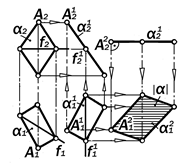
Задача № 2.2. Проекции плоской фигу-ры общего положения преобразовать в проекции этой же фигуры, находящейся в положении уровня (рис. 11.23).

Р ис.11.23. Графическое решение

метрической задачи № 2.2 ., п. а)

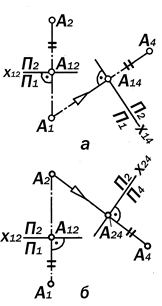
Рис. 11.24. Графическое решение

метрической задачи № 2.2 ., п. б)

Рис. 11.25. Замена одной плоскости

проекций для преобразования исходных проекций точки

Алгоритмы решений:

а) a ↷ a² || П₂ (рис.11.23);

1. a É f; f₁ ^ A₁ A₂ Ù Î a₁;

f₂ Î a₂;

2. f₂ ↷ f¹₂ || A₁A₂;

a₂ ↷ a¹₂;

a₁ ® a¹₁ - прямая линия;

3. a¹₁ ↷ a ²₁ ^ А₁ А ₂;

a¹₂ ® a²₂ =| a |.

б) a ↷ a² || П₁ (рис.12.24)

1. a É h; h₂ ^ A₁A₂ Ù Î a ₂;

h₁ Î a₁;

2. h₁ ↷ h¹₁ || A₁A₂;

a₁ ↷ (a¹₁ @ a₁);

a ₂ ® a¹₂ - прямая линия;

3. a¹₁ ↷ a²₁ ^ А₁А₂;

a²₁ ® a²₂ = | a |.

При помощи первой основной задачи на плоскость можно решать следующие конкретные метрические задачи:

1. Определить величину расстояния между точкой А и плоскостью a общего положения;

2. Определить величину расстояния между двумя параллельными плоскостями.

При помощи второй основной задачи на плоскость решаются следующие конкрет-ные метрические задачи:

3. Определить площадь плоской фигу-ры;

4. Определить все метрические харак-теристики плоской фигуры: её периметр, длины высот и сторон, углы при его вер-шинах и др.