Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие о метрических задачах
|
|
ГРАФИЧЕСКИЕ РЕШЕНИЯ
Понятие о метрических задачах
Определение 11.1. Метрическими называются задачи на определение натуральных значений тех или иных метрических характеристик геомет-рических объектов по их ортогональ-ным проекциям или наоборот, на пос-троение ортогональных проекций та-ких объектов пространства, метри-ческие характеристики которых на-перед заданы.
Из этого определения следует, что метрические задачи бывают прямыми и обратными.
Под метрическими характеристика-ми геометрических объектов понимают-ся их количественные меры.
Нульмерная точка внутренней мет-рики не имеет. Её положение в простра-нстве определяется внешней метрикой трёх её декартовых координат относи-тельно их начала.
Одномерная прямая линия облада-ет протяженностью в одном направле-нии и различной степенью наклонённо-сти к плоскостям проекций или укло-ном.
Отрезокпрямой линии имеет длину и
значения углов наклона к П1 и П2.
Двумерная плоскость обладает про-тяженностью в двух направлениях и
различной степенью её наклонённости к плоскостям проекций П1 и П2.
Плоская фигура имеет площадь и
| № п/п | Элементы пространства и их системы | Внутренняя метрика | Внешняя метрика |
| 1. | Точка А | -- | Координаты xA, уA, zA |
| 2. | Две точки А и В | Расстояние | AB | | A (x, y, z), B (x¢, y¢, z¢) |
| 3. | Прямая а | Протяженность | Ð а Н а1 = j ° илиÐ а F a2 = y ° |
| 4. | А Î а | | AH | или | AF | | Ð a H a1 = j ° или Ð a F a2 = y ° |
| А, В, Î а | | AB |; | AH |; | AF |; | BH |; | BF | | Ð a H a1 = j ° илиÐ a F a2 = y ° |
меры её конструктивных элементов, --
расстояния между её точками и парал-лельными прямыми, линейные углы
между её сторонами, величины угловеё наклона к плоскостям проекций.
Так как любой геометрический объ-ект является системой, то следует раз-личать метрику его структуры (т.е., вну-треннюю метрику) и метрику его поло-жения в пространстве (т.е., внешнюю метрику).
Определение 11.2. Внутренней ме-трикой геометрического объекта на-зывается совокупность количествен-
ных мер его структурных элементов и их взаимного расположения.
Определение 11.3. Внешней мет-рикой геометрического объекта назы-
вается совокупность количественных мер его положения относительно на-перед заданной системы отнесения.
В данном случае под системой от-несения следует понимать три взаимно-перпендикулярные плоскости проекций П1, П2 и П3, попарно пересекающиеся по трём взаимно-перпендикулярным осям проекций х12, y13, и z23, проградуиро-ванным метрически равными едини-цами измерения (в архитектурном и ди-зайнерском проектировании – милли-метрами). При этом за начало отсчета этих единиц принимается тройная точка О123 пересечения как плоскостей проек-ций, так и осей проекций.
Анализ определений 11. 2 и 11.3 по-казывает, что внутренняя и внешняя метрики объекта метризуют его пози-, ционные свойства, т.е., выступают как количественные характеристики его ка-чества. (рис.11.1)
Рис. 11.1. Таблица метрических
характеристик элементов
пространства и их простейших
систем (окончание)
| 6. | Отрезок АВ прямой а | | AB | | Ð AB T A1B1 = j° Ð АВ T А2В2 = y° |
| 7. | A, a | | A, a | - кратчайшее расстояние | А над, под, перед и за а |
| 8. | а || b | | a, b | - кратчайшее расстояние | Ð аНа1 =Ð bHb1 = j°; Ð aFa 2=Ð bFb2 = y ° |
| 9. | a ´ b = K | Ð a K b = m ° - угол между а и b при вершине К | Ð a H1 a1 = a °; Ð b H1 b1 = b °; Ð a F2 a2 = g °; Ð b F2 b2 = d °. |
| 10. | A ∸ b | | a, b | -- кратчайшее pасстояние между а и b | Ð a H a1 = a °; Ð а F а2 = b °; Ð b H b1 = g °; Ð b F b2 = d ° |
| 11. | a (△ ABC) | Ð BAC; Ð ABC; Ð ACB; | A, BC |; | B, AC |; | C, AB |; S – площадь∆ АВС | Ð a, П1 = j °; Ð a, П2 = y ° |
| 12. | К, a (△ АВС) | | K, a | - расстояние от К до a | K (x, y, z), Ð a, П1 = j °; Ð a, П2 = y °. |
| 13. | а || a | | a, a| - расстояние от а до a | Ð а Н а1; Ð а Fa2; Ð a, П1; Ð a, П2 . |
| 14. | а ´ a = К | Ð а, a - угол между а и a | Ð а Н а1; Ð а F а2; Ð a, П1 ; Ð a, П2 ; |
| 15. | a || b | | a, b | - кратчайшее расстояние | Ð a, b, П1, Ð a, b, П2 ; |
| 16. | a ´ b = а | Ð a, b - двугранный угол при ребре а | Ð a, П1 (П2), Ð b, П1 (П2). |
Для того, чтобы по ортогональным проекциям того или иного объекта оп-ределить те или иные его метрические характеристики, необходимо, чтобы эти проекции непосредственно содержали в себе необходимую метрическую инфор-мацию.
Рассмотрение метрического содер-жания изобразительных свойств проек-ций прямых линий и плоских фигур (см.
п.п. 9.3, 9.4) показывает, что такую ин-формацию непосредственно содержат в себе ортогональные проекции прямых и плоскостей частного положения.
Утверждение 11.1. Если в условие прямой метрической задачи входят проекции прямой линии или плоской фигуры частного положения (уровня или проецирующего), то соответст-вующая метрическая информация со-держится непосредственно в соот-ветствующих проекциях этих элемен-
тов и собственно решение такой за-
дачи сводится к снятию этой инфор-
мации без совершения каких бы то ни
было графических операций.
Утверждение 11.2. Если в условии прямой метрической задачи входят проекции прямой линии или плоской фигуры общего положения, то для её решения необходимо преобразовать эти проекции в проекции этих же эле-ментов, но находящихся в том или ином частном положении, с которых необходимая информация снимается непосредственно.
Такие преобразования исходных проекций возможны в двух случаях:
Случай 1: Если объект из общего по отношению к плоскостям проекций и неизменному направлению проецирова-ния положения п е р е м е щ а е т с я
в то или частное положение;
Случай 2, (основанный на принципе относительности движения): Если объ-ект неподвижен, а те или иные плоско-
сти проекций, не нарушая своей ортого-нальности, перемещаются из исходного
|
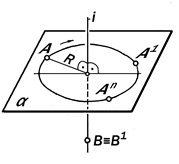
Рис. 11. 2. Геометрическая модель процесса вращения точки вокруг одной оси і
|
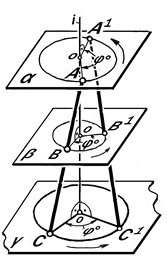
Рис. 11.3. Геометрическая модель
процесса вращения системы точек вокруг одной оси і
в такое положение, по отношению к ко-торому объект располагается в том или
ином частном положении.
Геометро-графическое моделиро-вание первого случая приводит к мето-ду п е р е м е щ е н и й [72], содержащему три способа, характер ко-торых определяется видом перемеще-ния объекта из общего положения в то или иное частное:
1. Если объект, перемещаясь, вра - щается вокруг оси, занимающей то или
иное проецирующее положение, то его исходные проекции преобразуются в искомые способом вращения вокруг проецирующих осей;
2. Если объект, перемещаясь, вра-щается вокруг оси, занимающей поло-жение линии уровня, то его исходные проекции преобразуются в искомые способом совмещения;
3. Если объект движется так, что все его точки перемещаются во вза-имно-параллельных плоскостях того или иного уровня, то его исходные про-екции преобразуются в искомые спосо - бом плоско-параллельного перемеще - ния.
Геометро-графическое моделиро-вание второго случая приводит к спосо - бу замены плоскостей проекций, су-щность которого заключается в пере-становке той или иной плоскости проек-ций из положения, не параллельного или не перпендикулярного к данному объекту, в положение параллельное или перпендикулярное к нему. При этом новое положение перемещённой плос-кости проекций должно быть перпенди-кулярным по отношению к той пло-скости проекций, которая оставалась неподвижной, а направление проециро-вания на перемещённую плоскость по-прежнему должно быть ортогональным.
Если возникает такая ситуация, при которой невозможно перемещать ни объект, ни плоскости проекций, то для преобразования исходных проек-ций объекта в искомые остаётся изме - нить направление проецирования.
В этом случае возникает способ вс - помогательного косоугольного прое - цирования. Его сущность заключается в том, что проецирующие лучи направля-
ются параллельно изображённым пря-
мым или плоскостям общего положения и тогда их исходные ортогональные
проекции преобразуются в вырожден-ные проекции (точки или прямые ли-нии), обладающие собирательным свойством. В силу этого способом вс-помогательного косоугольного проеци-рования решаются не метрические, а позиционные задачи.
В зависимости от того, на какие плоскости осуществляется вспомогате-льное проецирование, различают косо-угольное проецирование на основны е плоскости проекций и на четную бис-секторную плоскость.
|
|