💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Решение метрических задач

Рассмотренные выше процессы вращения прямой линии и плоской фи-гуры вокруг одной проецирующей оси

не позволяли преобразовывать проек-ции прямой общего положения в проек-ции её проецирующего положения, рав-но как проекции плоской фигуры обще-го положения в её проекции в положе-нии плоскости уровня. Для таких преоб-разований требовалось два последова-тельных вращения вокруг двух проеци-рующих осей.

Если принять в качестве оси вра-щения ту или иную линию уровня, то графическое решение этих задач резко упрощается за счет одного преобразо-вания исходных проекций в искомые и уменьшения числа графических опера-ций.

Геометрически ситуация представ-ляется следующим образом (рис.11.14):

Дано: П₁ – горизонтальная плоско-сть проекций; точка А и горизонтальная прямая h.

Требуется: Приняв горизонтальную прямую h за ось вращения і, повернуть вокруг неё точку А прежде до совмеще-ния с вертикальной плоскостью b, про-ходящую через h, а затем, - с горизон-тальной плоскостью g, также проходя-щей через h.

Решение: По законам вращения

точки вокруг прямой линии:

1. Плоскость a её вращения пер-пендикулярна к оси вращения. Так как эта ось горизонтальна, то эта плоскость вертикальна и вырождается на П₁ в пря-мую линию a₁ ^ і₁;

2. Центр О вращения точки А во-круг оси і является точкой их пересече-ния: О = a ´ і;

3. Радиусом R_A вращения точки А вокруг оси і является отрезок ОА в ис-ходном общем положении. Но, так как он вращается вокруг оси і вместе с точкой А, то в своём движении проходит два частных положения: вертикальное (ко-гда его горизонтальная проекция выро-ждается в точку и совпадает с О₁ ≡ h₁) и горизонтальное, (когда он проецируется

на П₁ в свою натуральную величину);

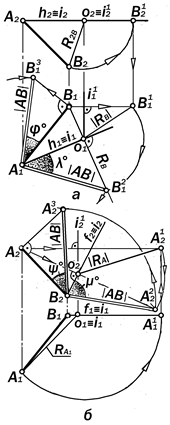
Рис11.15. Определение длины от-

резка АВ и углов его наклона к плоскостям проекций П₁ и П₂

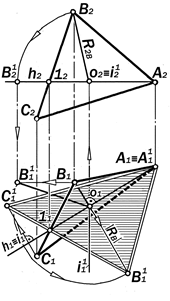
Р ис.11.16. Определение натуральной величины треугольника АВС для

вычисления его площади и других

метрических характеристик

4. Так как горизонтальная прямая h и не лежащая не ней точка А задают в пространстве некоторую плоскость s общего положения, то, подобно R_{A ,} вращаясь, эта плоскость проходит че-рез два частных положения: проециру-

ющее и уровня.

Из этих двух частных положений прямой и плоскости наибольший прак-тический интерес представляет поло-жение уровня, так как их проекции в таком положении содержат максимум информации об их внутренней метрике.

Вывод: Для того, чтобы графи-чески смоделировать момент совпа-дения вращающегося вокруг горизон-тальной оси отрезка ОА или плоской фигуры s с плоскостью уровня g, про-ходящей через эту ось, необходимо и достаточно отложить на горизонта-льном следе a₁ плоскости a вращения точки А от проекции О₁ натуральную величину радиуса её вращения и тем самым зафиксировать плоскость s в положении горизонтальной плоскости уровня.

11.3.1. Графические решения некоторых метрических задач способом совмещения

Задача №1. Определитьдлину отрезка АВ прямой а общего положения и углы его наклона к осям вращения h и f и плоскос-

тям проекций П₁ и П_2. (рис. 11.15, а, б).

Решение: 1. А Î (h º i) (рис.12.15, а)

h₂ ^ A₂ A_{1 ,} h₁ - произвольно;

А Î (h º i) Þ A º A¹ ;

2. B Î b ^ i; B₁ Î b₁ ^ i₁;

3. O = b ´ i; O₁ = b₁ ´ i₁; O₂ Î i₂;

4. OB = R_B; O₁B₁ = R₁, O₂B₂ = R _2;

5. O Î i¹ ^ П₂; і¹₂ º О₂, і₁ Î О₁ ‖ А₁ А₂;

6. R₂ ↷ R¹₂ ^ A₂ A₁; (B₁ ® B¹₁)^ A₂ A_{1 ;}

O₁ B¹₁ = | R_B |;

7. | R_B | ↷ | R¹ _B | º b ₁; A¹₁ B²₁ = | AB |,

(определяется в миллиметрах);

8. Ð | AB |, h₁ = | l ° |.

(определяется в градусах).

Для определения угла наклона отрезка АВ к плоскости П₁ необходимо и достаточно

принять проекцию А₁В₁ за прилежащий ка-тет прямоугольного треугольника, гипоте-нузой которого является натуральная вели-

чина | AB | отрезка АВ, и угол j ° между кото-рыми является искомым.

Для определения углов между отрезком АВ, осью вращения f º і и плоскостью П₂ не-обходимо прежде произвести все графичес-кие операции по нахождению его длины и угла наклона m° к f аналогично описанным в п.п. 2 – 8, а затем, приняв проекцию А₂В₂ за прилежащий катет прямоугольного треуго-льника, гипотенузой котрого является нату-оальная величина | AB | отрезка АВ и угол y °

между которыми является искомым.

Задача №2. Определить площадь треугольника АВС плоскости a общего положения (рис. 11.16)

Решение: 1. a É h;

h₂ ^ A ₂ A₁, h₁ É A₁ 1₁;

2. По алгоритму решения задачи № 1

(см. п.п. 2 – 7) горизонтальная проекция

А₁В₁ стороны А В общего положения преоб-разуется в проекцию А₁ В¹₁, равную нату-ральной величине стороны АВ, совпавшей с горизонтальной плоскостью уровня, прохо-дящей через горизонтальную ось вращения

і º h.

3. Так как вершина С конструктивно связана с вершиной В, то её горизонталь-ная проекция С₁, после преобразования В₁ в В¹_{1 ,} соответственно преобразуется в С¹₁ как точку пересечения горизонтального следа g ₁ плоскости её вращения с натуральной ве-личиной В¹₁ С¹₁ стороны ВС, определяемой точкой В¹₁ и точкой 1₁ её пересечения с осью вращения і.

Соединив С¹₁ с А₁, получаем треуголь-ник А₁ В¹₁С¹₁, конгруэнтный треугольнику АВС. Его площадь вычисляется как полу-произведение значения длины любой его стороны, принятой за основание, на значе-ние опущенной на неё высоты.

Следует особо отметить, что горизонта-льная проекция А₁В₁С₁ треугольника АВС и его натуральная величина являются род-ствеными фигурами, так как образуют де-заргову конфигурацию (см. рис.9.30).

 

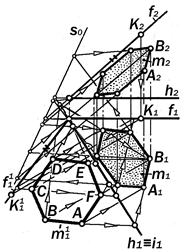
Задача №3. В плоскости a ( f ´ h ) общего положения изобразить правильный шестиугольник (рис.10.17)

 

Анализ условия: Так как данный прави - льный шестиугольник лежит в плоскости об-щего положения, то его ортогональные про-екции не являются правильными шестиуго-льниками. Поэтому для решения задачи следует прежде преобразовать проекции плоскости a общего положения в проекции

этой же плоскости в горизонтальном поло-

жении, затем изобразить в этом положении

Рис.11.17. Построение проекций правильного шестиугольника в плоскости общего положения

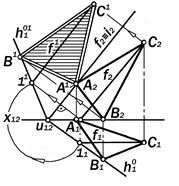
Рис. 11.18. Построение истинного вида плоской фигуры по её ортогональным проекциям вращением вокруг её фронтального следа

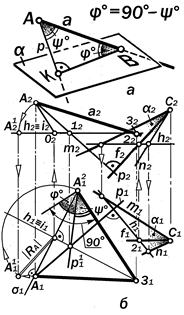
Рис. 11.19. Определение натуральной величины угла наклона прямой а к плоскости a

 

плоскости правильный шестиугольник и об-ратным преобразованием построить его искомые ортогональные проекции.

Решение: 1. Принять горизонталь h плоскости a за ось вращения: h º і;

2. Взяв на фронтали f произвольную то-чку К (К₂, К₁), повернуть её до совмещения с горизонтальной плоскостью уровня, проходящей через горизонталь h;

3. В совмещенном с плоскостью уровня положении плоскости a построить прави-льный шестиугольник АВСDEF;

4. Горизонтальную проекцию этого шес-тиугольника строить как фигуру, гомологич-ную его натуральной величине при оси го-мологии – оси вращения і и несобственном центре гомологии, ортогонально сопряжен-ном с её осью;

5. Искомую фронтальную проекцию ше-стиугольника строить как фигуру, гомологи-чную её горизонтальной проекции при на-правлении родства по линиям связи и оси гомологии, определяемой двумя точками пересечения разноименных проекций линий уровня f и h, задающих плоскость a.

Если не прибегать к аппарату гомоло-гии, то искомые проекции данного шести-угольника следует строить на основе гра-фического моделирования отношений при-надлежности его сторон и вершин к данной плоскости a.

Задача №4. Построить истинный вид плоской фигуры способом вращения во-круг её фронтального следа f⁰_{2 .} (рис.11.18).

Решение: По своему содержанию ре- шение этой задачи не отличается от ре-шений задач №2 и №3, а по форме неприн-ципиальное различие определяется тем, что осью вращения является фронтальный след данной фигуры, вращением вокруг ко-торого она совмещается с фронтальной плоскостью проекций.

Построения на рис.11.18 не требуют комментариев.

Задача №5. Определитьнатуральную величину угла наклона прямой а общего положения к плоскости a (m ´ n) общего положения a (рис.11.19, а, б)

Анализ условия: Известно, что уголме-жду прямой линией и плоскостью опре-деляется значением линейного между этой прямой и её ортогональной проекцией на эту плоскость. По условию данные плоско-сть и прямая занимают в пространстве об-щее положение и в общем случае пересека-ются к точке В (рис. 11.19, а). Для того, что-бы получить ортогональную проекцию а¢ прямой а на плоскость a, необходимо из точки А опустить на неё перпендикуляр р и найти его основание К. В полученном пря-моугольном треугольнике АКВ угол j ° меж-ду гипотенузой АВ и прилежащим катетом КВ будет искомым. Но, для того, чтобы по-строить его комплексный чертёж, необходи-мо на нем предварительно решить две позиционные задачи но построению точек В и К, что представляется громоздким.

Если обратить внимание на угол y ° ме-жду прямой а перпендикуляром р, то его значение будет дополнять значение иско-мого угла j ° до 90°. Поэтому, проведя в плоскости b (а ´ р) горизонталь h и по-вернув вокруг неё угол y ° при вершине А, до горизонтального положения, можно опре-делить значение угла j ° как разницу между углом 90° и дополнительным углом y °.

Решение: (рис. 11. 19, б):

1. А Î р ^ a;

А₁ Î р₁ ^ h°₁; А ₂ Î р₂ ^ f₂;

2. b (a ´ h) Î h º і

3. A₁ Î s₁ ^ h₁;

4. O₁ = s₁ ´ i_{1 ;} O₂ Î i₂;

5. OA = R_{A ;}

O₁ A₁ = R ₁ ; O₂ A ₂ = R ₂;

6. A ₂ O₂ ↷ A¹₂ ^ A₁ A _2;

A₁ ® A¹₁ ^ A _{1 A 2};

7. O₁ A¹₁ = R ¹₁ = | R |;

8. O₁ A²₁ = | R |;

9. Ð a¹₁ A²₁ p¹₁ = | y ° |;

10. j ° = 90 ° - y °

Задача №6. Определить натуральную ве-личину двугранных углов между плоскос-тями a (f_a ´ h_a) и b (f_b ´ h_b) общего положения. (рис.11. 20 .а, б).

Анализ условия: Известно, что двепло-скости, пересекаясь, образуют два разных по величине двугранных угла j ° и y °, в сумме составляющих 180°. Мерой любого из этих двугранных углов является линейный угол, стороны которого инцидентны его граням и перпендикулярны к его ребру. Для того, чтобы решить эту задачу, не строя проекций этого линейного угла, достаточно из точки А вне этих плоскостей опустить на них перпендикуляры р и q и вращением во-

круг линии уровня их плоскости определить натуральную величину угла между ними.

Этот угол будет дополнять искомый до 180°.

Решение: (рис. 11.20,. б).

1. А Î р ^ a; р₁ ^ h_{1 a}; p₂ ^ f _2a;

2. A Î q ^ b; q₁ ^ h_{1 b}; q₂ ^ f_{2 b};

3. s (р ´ q) É h º і;

4. см. п.п 4 – 9 решения задачи №5;

10. j ° = 180° - y °

Рис. 11.20. Определение натуральной величины двугранного угла между двумя плоскостям общего положения

Рис.11.21. Графическое решение первой

основной задачи на прямую, п. 1.1.

 

 

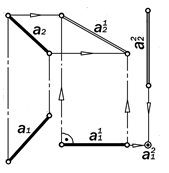
Рис. 11.22. Графическое решение второй основной задачи на прямую,

п. 1.2.

⇐ Предыдущая12345678Следующая ⇒