Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Преобразования как изменение координатных систем

На первой лекции мы рассматривали геометрический конвейер и говорили о различных координатных системах и переходах между ними. В данной лекции мы говорим о преобразованиях геометрических объектов. Как же устранить данное противоречие?

Рассмотрим любое преобразование объекта, например перенос точки. Перенесем точку в соответствии с заданным вектором. Как показано на рис 2.16 а. точка Р с координатами (2 3) преобразуется в точку Р’ с координатами (4 5).

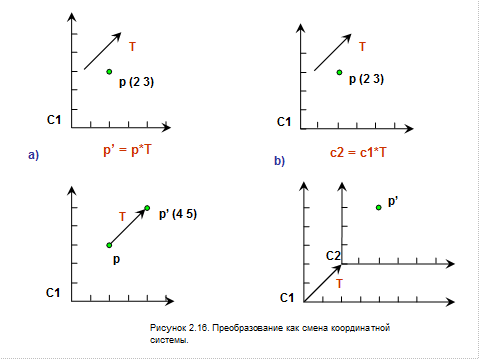
Данную ситуацию можно трактовать иначе. Точка осталась неизменной, а изменению подверглась вся координатная система. Таким образом, мы с помощью преобразования сдвига преобразовали координатную систему С1 в координатную систему С2.Координаты точки в системе C2 остались (2, 3) а С1 изменились на (4, 5).

Такой взгляд можно рассматривать как метафору, потому что для реализации перевода сцены из одной координатной системы в другую необходимо подвергнуть преобразованию каждый объект сцены. Мы используем такую нотацию, так как в терминах координатных систем и их преобразований легче объяснять устройство и работу графических систем, а так же писать программы. В этом мы убедимся позже при написании программ с использованием OpenGL.

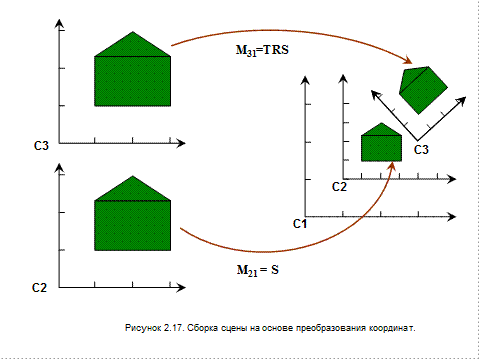
Рассмотрим еще один пример. В исходной координатной системе С1 с помощью преобразования масштабирования (Sx=0.5 Sy=0.5) определим координатную систему C2=C1*S₂₁. На ее основе с помощью преобразований переноса (Dx=4 Dy=2) и поворота (q=45º) определим координатную систему C3=C2*T₂₃*R₂₃. С учетом композиции запишем С3=С2*M₂₃. Очевидно, что отношения между координатными системами С3 и С1 описываются формулой C3= C1*S₂₁*T₂₃*R_{23 =}С1*М₃₁.

Таким образом, мы определили три координатные системы и установили отношения между ними. Нарисуем в координатных системах С2 и С3 два одинаковых домика и перейдем в координатную систему С1. Изображения подверглись масштабированию, повороту и смещению согласно установленных нами отношений. Результат выполненных действий показан на рисунке 2.17

Этот простой пример демонстрирует важный этап визуализации – сборку сцены. В процессе сборки мы определяем фрагменты сцены в координатных системах, удобных для построения. Обычно такие координатные системы в графическом конвейере носят название модельных координат. В некоторых источниках, дающих более строгое математическое обоснование, используют термин фрейм.

После определения всех необходимых фрагментов производят преобразование всех модельных координатных систем в единую систему, носящую название мировых координат.

Заключение.

Мы рассмотрели наиболее часто используемые геометрические преобразования - поворот, перенос и масштабирование. Их представление в матричной форме дает возможность провести композицию преобразований и представить несколько преобразований одной матрицей. При создании композиции преобразований необходимо учитывать не коммутативность преобразований.