Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Выводы по плоским геометрическим преобразованиям

Подводя итог изучению двумерных преобразований, еще раз обратим внимание на структуру матрицы преобразования.

М =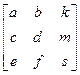

Элементы a, b, c и d определяют коэффициенты поворота, масштабирования и сдвига. Элементы е и f служат для формирования переноса. Смысл трех оставшихся элементов необходимо прояснить. Начнем с k и m. Обычно мы устанавливали им нулевое значение. Теперь положим их отличными от нуля, элементы главной диагонали приравняем к единице, а остальные элементы обнулим. Применим получившееся преобразование к произвольной точке, заданной в однородных координатах с w =1.

[x’ y’ w’] = [x y 1] 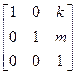= [x y kx+my+1]

x’ = x, y’=y

Для того чтобы понять результат, обратимся к геометрической интерпретации однородных координат. Точка в однородных координатах определяется тройкой, следовательно, мы имеем дело с трехмерной координатной системой, определенной в пространстве. Две оси системы нам привычны - это X и Y, а третья – W, ось масштабных коэффициентов. Зафиксировав значение W, установив его равным единице, мы перешли от пространства к плоскости параллельной плоскости XOY. Установив элементы k и m отличными от нуля, мы сняли данное ограничение, и полученная в результате преобразования точка расположена в пространстве. При этом ее третья координата определяется по формуле kx+my+1, т.е. зависит от значений x и у. Следовательно, точки, подвергшиеся данному преобразованию, будут лежать в некоторой плоскости не параллельной плоскости XOY, как это показано на рис 2.12.

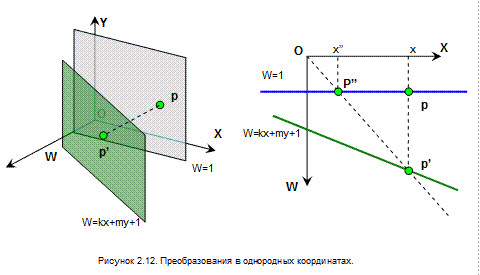
Вернем точку на плоскость W=1 путем проецирования лучами, проходящими через начало координат. Из подобия треугольников x’’= x’/w’= x/(kx+my+1) и аналогично y’’= y’/w’= y/(kx+my+1). Таким образом, математически подобное проецирование выразится в простой нормализации.

[x’’ y’’ 1] =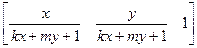

Для выяснения смысла элемента s матрицы преобразования, проведем рассуждения по аналогичной схеме. Умножим произвольную точку на соответствующую матрицу с ненулевым значением s.

[x y 1] 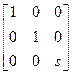= [x y s]

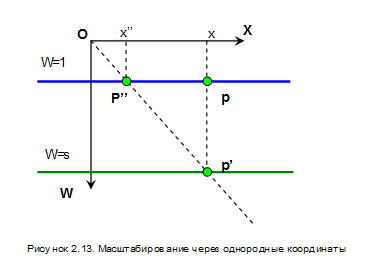
Все точки, подвергшиеся такому преобразованию, будут лежать в плоскости W=s которая параллельна плоскости W=1, как это показано на рисунке 2.13. Нормализация будет приводить к простому масштабированию с одинаковыми коэффициентами по осям.

[x’ y’ 1] =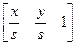

Основное отличие такого масштабирования от рассмотренного ранее состоит в том, что при s< 1 будет происходить растяжение, а при s> 1 – сжатие.