Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Преобразование поворота

Рассмотрим следующее преобразование 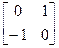. Его результат можно рассматривать как поворот на 90 градусов против часовой стрелки относительно начала координат (см. рис. 2.6). Нетрудно определить другие частные случаи поворота: на 180 - 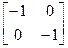и 270 градусов - .

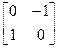Но как определить преобразование поворота относительно начала координат на произвольный угол? Рассмотрим схему такого поворота, представленную на рисунке 2.7.

Введем следующие обозначения: r – радиус поворота. Отрезок ОР, соединяющий начало координат О с поворачиваемой точкой Р; l - угол между осью x и начальным положением отрезка ОР; q - угол, на который выполняется поворот. Определим начальное положение точки Р и ее положение после поворота Р’.

Р = [x y] = [r cos l r sin l] (1)

Р’ = [x’ y’] = [r cos(q+l) r sin(q+l)]

Применив формулы косинуса и синуса суммы, получим:

Р’ = [x’ y’] = [r(cos q cosl - sin q sinl) r(sin q cos l+ cos q sin l)]

Раскрывая скобки и учитывая формулу (1), получаем:

Р’ = [x’ y’] = [(xcos q - y sin q) (x sin q + y cos q)] т.е. точка после поворота имеет координаты

x’ = x cos q - y sin q

y’ = x sin q + y cos q

Переходя к матричному представлению, получаем матрицу преобразования поворота на произвольный угол q относительно начала координат:

R =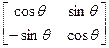

Для обращения преобразования необходимо выполнить поворот в противоположную сторону на тот же угол.

R^-1 = 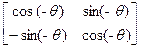=