Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Преобразование масштабирования

Вернемся к общей схеме преобразования и рассмотрим ряд частных случаев преобразования и их геометрический смысл.

Положим c=b =0, a¹ 0 и d ¹ 0, тогда

Р*М =[x y] 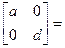[(ax+0y) (0x+dy)] =[(ax) (dy)]= [x’ y’]

Таким образом

x’= ax

y’= dy

Следовательно, мы получили преобразование масштабирования. Коэффициенты a и d являются масштабирующими коэффициентами по осям x и y. Обычно их обозначают Sx и Sy, а соответствующая матрица носит название матрицы масштабирования.

S =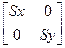

Если 0 < Sx = Sy < 1 имеет место сжатие, в противном случае при Sx = Sy > 1 будет иметь место расширение. Примеры масштабирования приведения на рис. 2.1. Обратите внимание, что при масштабировании геометрических объектов происходит не только изменение их размеров, но и смещение относительно начала координат.

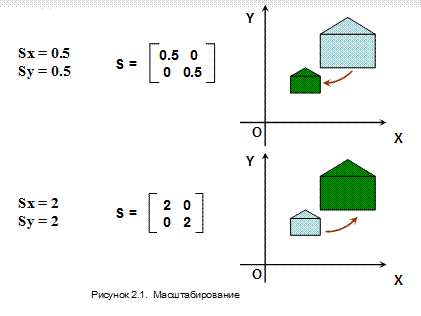
Начало координат остается инвариантным как к преобразованию масштабирования, так и к другим преобразованиям, выполняемым по рассматриваемой схеме. В этом легко убедится:

[0 0] 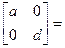[(a*0+0*0) (0*0+d*0)] =[(0) (0)]= [0 0]

Если Sx ¹ Sy, то координаты масштабируются различным образом, и происходит искажение пропорций объектов как это видно на рисунке 2.2.

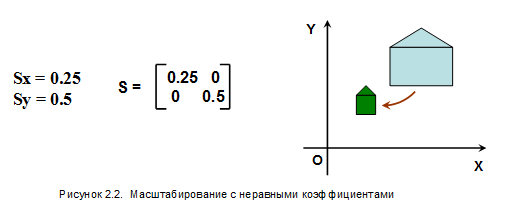
Для обращения преобразования необходимо произвести масштабирование с коэффициентами, обратными заданным. Обратная матрица представляется следующим образом: S^-1 =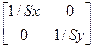

Интересный эффект возникает при разрешении отрицательных значений коэффициентов в матрице масштабирования. В этом случае, наряду с масштабированием происходит отображение объектов относительно различных осей. Положим Sx = -2, а Sy = 1.

S= 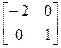x’= -2*x y’= 1*y

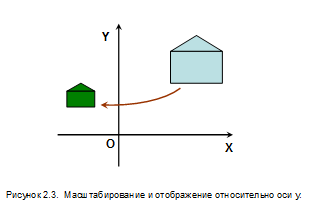
Очевидно, что координата y останется неизменной, а координата x увеличится вдовое и поменяет свой знак, т.е. наряду с масштабированием произойдет отображение относительно оси y.

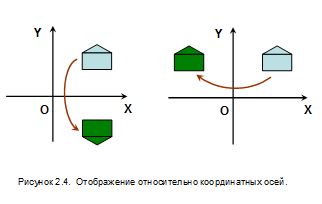
При единичных величинах коэффициентов масштабирования не будет, а знаки будут определять оси отображения. Матрица 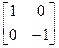определит отображение относительно оси х, а матрица 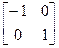- отображение относительно оси y. Результаты подобных преобразований показаны на рис 2.4.

Если отклониться от условий масштабирования, положив 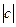= =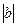1 и a=d=0, тогда

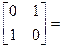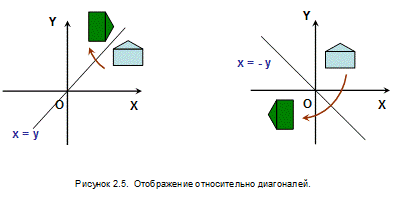
преобразование [x y] [(0x+1y) (1x+0y)] =[(y) (x)]= [x’ y’] приведет к перестановке координат x’= y, y’= x, что геометрически можно представить как отражение относительно прямой x=y, делящей первый квадрант на октанты. Преобразование 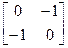приводит к отображению относительно прямой y = -x. Примеры преобразований показаны на рис 2.5.