Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Преобразования поворота в пространстве

Повороты в пространстве производятся вокруг осей. Рассмотрим повороты вокруг главных координатных осей. Положительными считаются повороты против часовой стрелки, если смотреть с конца положительной полуоси. Изученный нами ранее поворот относительно начала координат на плоскости XOY можно рассматривать как поворот в пространстве относительно оси Z. Для получения матриц поворота относительно других координатных осей можно использовать ту же схему рассуждений, что приводилась нами для определения поворота на плоскости XOY.

Повороты вокруг произвольных осей строятся за счет композиции поворотов вокруг главных координатных осей. Схема такого подхода нами уже разбиралась. Применим ее на практике еще раз.

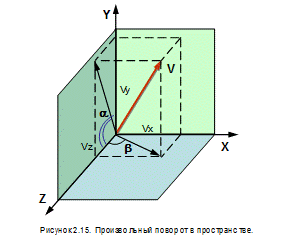
Сначала уточним исходные данные. Для задания произвольного поворота в пространстве недостаточно определить только ось. При этом невозможно определить направление поворота. Необходимо задать направляющий вектор и точку его привязки. Так же необходимо задать величину угла поворота q.

Для выполнения заданного преобразования необходимо:

· Совместить точку привязки с началом координат за счет преобразования переноса Т, задаваемого вектором, соединяющим начало координат с этой точкой. В результате приходим к ситуации показанной на рисунке 2.15.

· Выполнить поворот вокруг оси X на угол a, переводящий направляющий вектор в плоскость XOZ.

· Выполнить поворот вокруг оси Y на угол b, совмещающий направляющий вектор с положительной полуосью Z.

· Выполнить поворот вокруг оси Z на требуемый угол q.

· Выполнить обратные преобразования, приводящие сцену в исходное состояние.