Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Моделей в направлении радиальной координаты r

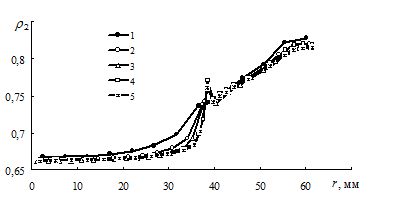
Р и с. 4.9. Влияние размеров сетки на распределение плотности оболочки по радиусу r 2(r) (обозначения – в табл. 4.2)

Размеры областей с малыми градиентами плотности пропорциональны размерам плоских границ. Протяженность плоской границы с заготовкой в осевом направлении (высота заготовки h ₁) значительно меньше, чем в радиальном направлении (радиус заготовки R ₁), и область с малым градиентом плотности практически отсутствует. Поэтому в радиальном направлении задавалась неравномерная сетка с большой величиной h_r в области малых градиентов и с уменьшением размера h_r в области высоких градиентов плотности. В осевом направлении дискретизация осуществлялась равномерной сеткой с одинаковым размером h_z по всей высоте деформируемого объема.

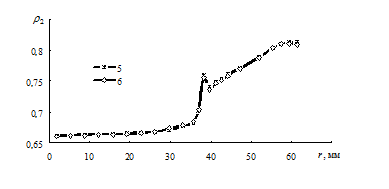
Расчеты показали (см. рис. 4.9 и 4.10), что численные решения по распределению плотности r ₂(r) и r ₂(z) сходятся при размерах сетки, соответствующих вариантам 4 и 5 дискретизации на конечные элементы. Согласно правилу Рунге искомые значения пространственных координат, обеспечивающие заданную точность решения, соответствуют модели 5, имеющей более крупную сетку, чем модель 4. С целью сокращения времени расчета по модели 5 была построена модель 6. Ее параметры были получены путем выбора максимальных значений h_r и h_z из дискретных моделей 4 и 5. Кроме того, в модели 6 по сравнению с моделью 5 была увеличена высота сетки конечных элементов h_z в заготовке. Результаты решения по модели 6 практически не отличаются от результатов решений по модели 5 (рис. 4.11 и 4.12). Вместе с тем время расчета уменьшается в 1, 5 раза. Таким образом, окончательные оптимальные размеры сетки конечных элементов, обеспечивающие заданную точность решения краевой задачи пластического деформирования, соответствуют дискретной модели 6 (табл. 4.2).

Р и с. 4.11. Распределение плотности оболочки по радиусу r 2(r) для моделей 5 и 6

Итоговые размеры пространственных координат h_r, h_z сетки конечных элементов получены для конкретных размеров заготовки и оболочки и в определенной степени имеют частный характер. Вместе с тем можно выделить параметры, которые будут инвариантны к изменению каких-либо размеров заготовки или оболочки. При уменьшении размеров инвариантами могут служить топологические характеристики дискретной модели. Для рассмотренных размеров заготовки и оболочки модели 6 соответствуют следующие 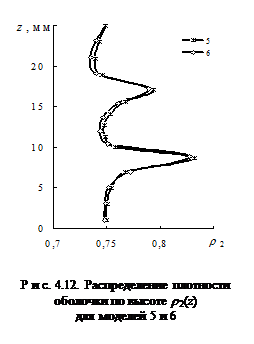топологические параметры: Ns 1 = 6; Ns 2 n = Ns 2 v = 4; Nr 1= 14; Nr 2 = 24. Эти значения можно использовать при уменьшении какого-либо размера заготовки или оболочки. При увеличении размеров по сравнению с размерами модели 6 следует сохранять размеры сетки в областях с высокими градиентами плотности. Для заготовки это значения h_r =1, 33 мм в пределах 4 мм от боковой поверхности и h_z =2, 33 мм в пределах 7 мм от опорных плоскостей; для оболочки – h_r =1, 5 мм в пределах первых 6 мм от боковой поверхности заготовки; h_r =2 мм в пределах 8 мм от боковой поверхности матрицы с трением и h_z =2, 33 мм в пределах первых 10 мм от опорных плоскостей заготовки. Расчеты показали, что при удалении от опорных плоскостей заготовки свыше 10 мм шаг h_z можно увеличить до значения h_z =5 мм.

Выше были определены размеры сетки конечных элементов для изотермической задачи пластического деформирования. Размеры сетки конечных элементов при решении задач нестационарного теплообмена и пластического деформирования отличаются друг от друга. При решении задачи неизотермического пластического деформирования из двух дискретных моделей выбирается модель с более мелкой сеткой. В связи с большими градиентами температур размеры приграничных элементов заготовки и оболочки в тепловой задаче меньше, чем размеры соответствующих элементов в задаче механики. Так, в задаче теплообмена толщина первых трех слоев, начиная с контактного слоя, составляет 0, 5; 1, 5 и 2 мм в заготовке и 0, 25; 0, 75 и 2 мм в оболочке. В задаче механики минимальные размеры конечных элементов в заготовке и оболочке соответственно равны 1, 33 мм и 1, 5 мм, поэтому в дальнейшем при решении неизотермической задачи пластического деформирования использовались размеры сетки, соответствующие решению задачи нестационарного теплообмена.