Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
При центральном зажигании
|
|
Схема распространения фронта горения при зажигании из центра круглой пластины показана на рис. 2.15.
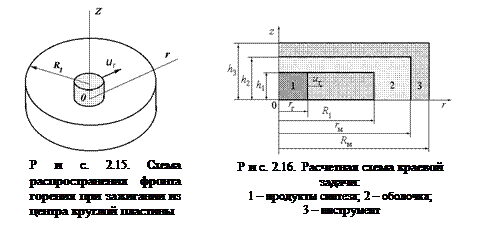
Физическая задача согласно расчетной схеме, приведенной на рис. 2.16, формулируется следующим образом. Круглая заготовка толщиной 2 h 1 и радиусом R 1 помещена в песчаную оболочку и стальную цилиндрическую матрицу. Размеры оболочки и матрицы известны. В начальный момент времени в центре заготовки инициируется реакция горения с известной температурой горения Т г и скоростью горения u г. Объект моделирования представляет собой трехэлементную осесимметричную систему с областями конечных размеров и с внутренней подвижной границей первого рода (фронт горения). Между элементами системы происходит нестационарный теплообмен. Теплообмен продуктов синтеза с оболочкой и оболочки с инструментом осуществляется при граничных условиях четвертого рода с идеальным тепловым контактом. На границе «инструмент-окружающая» среда имеют место граничные условия третьего рода. Фронт горения считается плоским и адиабатическим. Требуется найти температурное поле системы трех соприкасающихся тел в произвольный момент времени t. В связи с осевой симметрией рассматривается четвертая часть меридионального сечения в цилиндрических координатах r и z.
Математическая постановка задачи осесимметричного теплообмена на стадии горения включает:
1) систему трех дифференциальных уравнений нестационарной теплопроводности в цилиндрических координатах
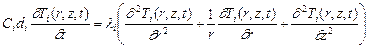; (2.34)
2) граничные условия:
на границах «заготовка-оболочка» (z = h 1) и «оболочка - инструмент» (z = h 2 и r = r м) – условия четвертого рода
l 1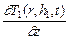 
= l 2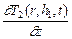 
; T 1(r, h 1, t) = T 2(r, h 1, t); (2.35)
l 2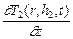 
= l 3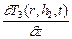 
; T 2(r, h 2, t) = T 3(r, h 2, t);
на границе «инструмент-окружающая» среда (z = h 3 и r = R м) – условия третьего рода (конвективный теплообмен)
l 3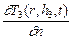 
+ a т[ T 3(r, h 3, t) - T s] = 0; (2.36)
l 3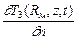 
+ a т[ T 3(R м, z, t) - T s] = 0;
3) начальные условия
Т 1(0, z 1, 0) = T г; Т 2(r, z, 0) = Ts; Т 3(r, z, 0) = Ts; (2.37)
4) уравнение движения фронта горения
r г = u г t; (2.38)
5) температуру подвижной границы первого рода (фронт горения)
Т 1(r г, z 1, t) = Т г ; (2.39)
6) условие адиабатичности перед фронтом горения
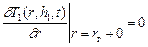; (2.40)
7) условие симметрии температурного поля относительно осей
z и r
; 
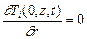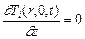. (2.41)
При расчете температурного поля после сгорания всего объема шихты из системы уравнений (2.34)-(2.40) исключаются уравнения (2.38)-(2.40) и добавляются граничные условия четвертого рода на цилиндрической поверхности заготовки при r = R 1:
l 1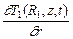 
= l 2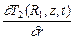 
; T 1(R 1, z, t) = T 2(R 1, z, t). (2.42)
В уравнениях (2.34)-(2.42) введены следующие обозначения: Тi – температура тел; Сi, di, li – удельная теплоемкость, гравиметрическая плотность и коэффициент теплопроводности тел системы; hi – характерные размеры тел системы (см. рис. 2.16); i – индекс тела системы: 1 – продукты синтеза, 2 – оболочка, 3 – пуансон; t – время; r г – радиус фронта горения; r м, R м – внутренний и наружный радиусы матрицы; a т – коэффициент теплоотдачи; ТS – температура среды; n – нормаль к граничной поверхности.
Поставленная осесимметричная краевая задача нестационарного теплообмена решалась методом конечных элементов при минимизации функционала Дьярмати. имеющего в цилиндрических координатах следующий вид [171]:
J =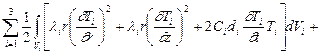 
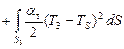, (2.43)
где Vi – объем тел системы; S 3 – площадь инструмента с конвективным теплообменом. На стадии горения объем V 1 горячих продуктов синтеза, с которыми происходит теплообмен, является функцией времени:
. (2.44)
Численное решение осесимметричной задачи осуществлялось по алгоритму численного решения плоской задачи нестационарного теплообмена, который был рассмотрен в разд. 2.2. Зависимость теплофизических свойств продуктов синтеза и песчаной оболочки от температуры не учитывалась, и решалась физически линейная краевая задача. Для дискретизации объекта использовались кольцевые осесимметричные элементы треугольного сечения и линейная аппроксимация температуры внутри каждого элемента [171]. При разбиении на конечные элементы вся область сначала покрывалась прямоугольной сеткой, а затем полученные прямоугольники диагоналями делились на два треугольника. В областях границ контактного теплообмена заготовки и оболочки с высокими градиентами температуры выполнялось сгущение сетки КЭ. Элементы матриц теплопроводности [L], теплоемкости [ C ] и вектора тепловых нагрузок { Fk } вычисляли по известным зависимостям для кольцевых элементов треугольного сечения [171]. Для дискретной модели осесимметричной задачи принимались такие же значения пространственно-временных координат, что и для дискретной модели плоской задачи. При этом общее число узлов составляло Nu = 299; число элементов Ne = 528.
|
|