
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач. Задача 1.Положительные заряды q1 = 2мкКл и q2 = 10мкКл находятся в вакууме на расстоянии 1м друг от друга
|
|
Задача 1. Положительные заряды q 1 = 2мкКл и q 2 = 10мкКл находятся в вакууме на расстоянии 1м друг от друга. Определить работу, которую совершат силы отталкивания при удалении заряда q2 на расстояние 10м от заряда q1.
| Дано: q 1= 2мкКл q 2 = 10мкКл r 1 = 1м r 2 = 10м | 2× 10-6Кл 10-5 Кл | Решение. Рассмотрим физическую систему состоящую из двух зарядов q 1 и q 2 и их поля. Будем считать заряд q 1 неподвижным. Заряд q 2 под действием поля заряда q 1 перемещается из точки В в точку С. |
| А -? |
Расстояние от точки В до заряда q 1 равно r 1, потенциал поля в этой точке j1. Расстояние от заряда q 1 до точки С равно r 2, потенциал поля в точке С равен j2. Тогда работа совершаемая при перемещении заряда q 2 из точки В в точку С равна (2.7):
A = q 2(j1 -j2). (2.8)
где j1 и j2 в соответствии с (2.2):
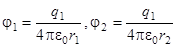 . (2.9)
. (2.9)
Подставим (2.3) в (2.2):
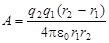 . (2.10)
. (2.10)
После подстановки числовых значений получили: А = 0, 162 Дж.
Ответ: 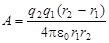 =0, 162 Дж.
=0, 162 Дж.
Задача 2. Найти работу поля по перемещению заряда q = 10 нКл из точки 1 в точку 2 (рис. 2.2), находящиеся между двумя разноименно заряженными с поверхностной плотностью s =0, 4мкКл/м2 бесконечными параллельными плоскостями, расстояние между которыми равно 3см.
| Дано: q = 10 нКл s =0, 4 мкКл/м2 l = 3 см | 109 Кл 4·10-7 Кл/м2 0, 03 м | Решение. Решим задачу двумя способами. |
| А -? |
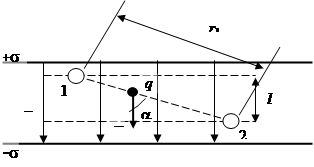

Рис.2.2
1-й способ. Работу сил поля по перемещению заряда q из точки 1 с потенциалом j1 в точку 2 с потенциалом j2 найдем по формуле (2.7):
A = q (j1 -j2). (2.11)
Разность потенциалов j1 -j2 найдем из (2.6):
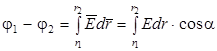 . (2.12)
. (2.12)
Поле между двумя равномерно заряженными параллельными плоскостями однородно и его напряженность равна:
 . (2.13)
. (2.13)
Подставим (2.13) в (2.12) и после интегрирования получим (см. рис.2.2):
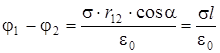 . (2.14)
. (2.14)
Тогда работа будет определяться выражением:
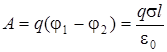 (2.15)
(2.15)
2-й способ. При перемещении тела под действием силы ` F совершается работа:
 . (2.16)
. (2.16)
Сила, действующая на заряд в электрическом поле с напряженностью (2.13), будет равна:
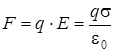 (2.17)
(2.17)
Подставим (2.17) в (2.16) и проинтегрируем:
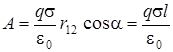 (2.18)
(2.18)
Оба решения приводят к одному и тому же результату. После подстановки в (2.18) числовых значений получим: А = 13, 6 мкДж.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Ответ: 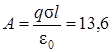 мкДж.
мкДж.
Задача 3. Найти потенциал в центре кольца, по которому равномерно распределен заряд с линейной плотностью t.
| Дано: t | Решение. Физическую систему составляют равномерно заряженное кольцо и электрическое поле этого заряда. Для определения потенциала j в центре полукольца воспользуемся |
| j -? |
 принципом суперпозиции. Разделим полукольцо на малые элементы дуги dl так, чтобы заряд dq = t dl каждого такого элемента можно было считать точечным (см. рис.2.3). Тогда потенциал поля, создаваемого зарядом dq, будет равен (2.2):
принципом суперпозиции. Разделим полукольцо на малые элементы дуги dl так, чтобы заряд dq = t dl каждого такого элемента можно было считать точечным (см. рис.2.3). Тогда потенциал поля, создаваемого зарядом dq, будет равен (2.2):
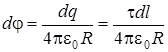 . (2.19)
. (2.19)
Согласно принципу суперпозиции потенциал в центре полукольца определяется алгебраической суммой потенциалов d j элементарных зарядов:
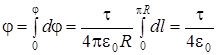
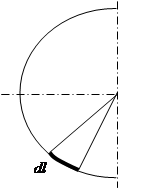
Рис.2.3
Ответ: 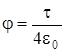
Задача 4. Поле образовано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда s = 4× 10-8Кл/м2. Определить разность потенциалов двух точек поля, стоящих от плоскости на r 1 = 10см и r 2 = 20см (рис 2.4).
| Дано: s = 4× 10-8Кл/м2 r 1 = 10см r 2 = 20см | 0, 1м 0, 2 м | Решение.
Физическую систему составляют бесконечная равномерно  0, 2м заряженная плоскость и созданное ней электрическое поле. Для определения разности потенциалов используем связь напряженности и потенциала (2.6): 0, 2м заряженная плоскость и созданное ней электрическое поле. Для определения разности потенциалов используем связь напряженности и потенциала (2.6):
|
| (j1-j2) -? |

Рис. 2.4
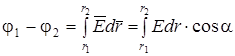 . (2.20)
. (2.20)
Так как точки 1и 2 расположены на одной силовой линии cos 0 =1. Следовательно, с учетом (1.10) Е = s/2e°, получим:
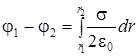 ,
,
или после интегрирования
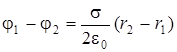 . (2.21
. (2.21
После подстановки числовых значений получим: j1-j2 =225 В.
Ответ: 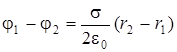 =225 В.
=225 В.
Задача 5. Электрон движется в плоском горизонтально расположенном конденсаторе параллельно его пластинам со скоростью υ = 4× 107м/с. Разность потенциалов на пластинах конденсатора U = 4кВ, расстояние между пластинами d = 4см, длина пластин конденсатора l = 20см. На какое расстояние сместится электрон в вертикальном направлении под действием электрического поля во время его движения в конденсаторе.
| Дано: υ = 4 × 107 м/с U = 4000 В d = 4× 10-2 м l = 0, 2 м | Решение.
Рассмотрим движение электрона между пластинами конденсатора (см. рис.2.5). Электрон будет двигаться под действием двух сил: силы тяжести m 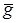 и электрической силы` Fэл = е и электрической силы` Fэл = е 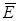 . Можно заметить, что ½ mg ½ < < ½ еЕ ½, т.к. mэл =9, 1× 10-31 кг, а е = -16× 10-19 Кл. . Можно заметить, что ½ mg ½ < < ½ еЕ ½, т.к. mэл =9, 1× 10-31 кг, а е = -16× 10-19 Кл.
|
| h -? |
Поэтому действием силы тяжести в данном случае можно пренебречь. Согласно второму закону Ньютона запишем:
m 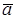 = e
= e 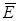 . (2.22)
. (2.22)
Выберем ось x так, чтобы она была параллельна пластинам конденсатора, а y – перпендикулярна (см. рис.2.5). Выражение (2.22) в проекциях на ось y будет иметь вид:
ma = | eE |(2.23)
 |  |  |  |  |  |  | |||||||||||
 |  | ||||||||||||||||







 О
О
 | ||||||
 | ||||||
 | ||||||
 | ||||||
Рис. 2.5
Напряженность поля внутри конденсатора связана с разностью потенциалов, как следует из (2.6), выражением:
U = Ed (2.24)
Из (2.23) и (2.24) найдем а = ау:
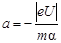 .(2.25)
.(2.25)
Так как ускорение электрона постоянное, его перемещение будет равно:
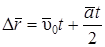 , (2.26)
, (2.26)
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
 или в проекциях на оси Ох и Оу соответственно:
или в проекциях на оси Ох и Оу соответственно:
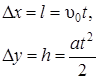 . (2.27)
. (2.27)
Решим уравнение (2.27) с учетом (2.25):
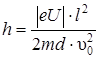 . (2.28)
. (2.28)
Подставим в (2.28) числовые значения и получим: 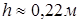
Ответ: 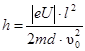
 .
.
Задача 6. Два одноименных точечных заряда q 1 и q 2 с массами m 1 и m 2 движутся на встречу друг другу. Когда расстояние между ними равно r 1, их скорости равны υ 1 и υ 2. До какого минимального расстояния r min сблизятся заряды?
| Дано: q 1 q 2 m 1 m 2 r 1 υ 1 υ 2 | Решение. Рассмотрим замкнутую физическую систему состоящую из двух электрических зарядов q 1 u q 2. По закону сохранения энергии энергия системы W 1 в момент, когда заряды находились на расстоянии r, должна быть равна энергии W 2 в момент максимального сближения зарядов. В этот момент времени заряды в следствие действия электрических сил отталкивания остановятся, их кинетическая энергия будет равна нулю. В начальный момент, когда заряды двигались со скоростями υ 1 и υ 2, энергия системы складывалась из кинетической энергии W 1к и потенциальной энергии взаимодействия зарядов (2.4): |
| r min-? |

Следовательно:
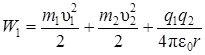 . (2.29)
. (2.29)
В момент, когда расстояние между зарядами стало r min, энергия системы представляла собой только потенциальную энергию взаимодействия зарядов:
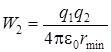 , (2.30)
, (2.30)
т.к. W 1= W 2, получим, приравняв (2.29) и (2.30) и выразив r min:
 .
.
Ответ: 
Задача 7. Электрическое поле создано длинным цилиндром радиусом R =1см, равномерно заряженным с линейной плотностью t =20нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстояниях а 1 =0, 5см и а 2 = 2см от поверхности цилиндра, в средней его части.
| Дано: R =1см t =20нКл/м а 1 =0, 5см а 2 = 2см | 10-3 м 2·10-8 Кл 5·10-3 м 2·10-2 м | Решение. Рассмотрим физическую систему, состоящую из заряженного цилиндра и создаваемого им поля. Для определения разности потенциалов используем соотношение (2.12): |
| (j1-j2) -? |
 , (2.31
, (2.31
т.к. цилиндр длинный и точки взяты вблизи его средней части, то напряженность поля в этих точках будет близка к напряженности поля, создаваемого равномерно заряженной бесконечной прямой нитью (1.11):
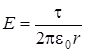 . (2.32)
. (2.32)
Считая точки, в которых ищем потенциал, расположенными вдоль одной силовой линии из (2.31) и (2.32) получим:
 . (2.33)
. (2.33)
После интегрирования, с учетом того, что r 1= R+a 1 и r 2= R+a 2, будем иметь:
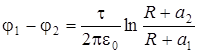 .
.
После подстановки числовых значений получим: j1-j2 = 250 В.
Ответ: 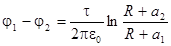 = 250 В.
= 250 В.
Задача 8. Найдите электроёмкость батареи конденсаторов, изображённой на рис.3.1.
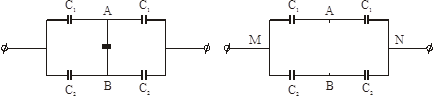
Рис. 3.1. Рис.3.2
| Дано: С 1 С 2 | Решение.
Рассмотрим физическую систему, состоящую из пяти конденсаторов, соединенных в батарею. Вследствие симметрии цепи потенциалы точек А и В (рис.3.1) одинаковы, т.е. напряжение на конденсаторе С2 будет равно нулю:  . Значит, конденсатор С2 не . Значит, конденсатор С2 не
|
| С -? |
заряжен, и можно считать, что между точками А и В участок отсутствует (разрыв цепи). Эквивалентная цепь изображена на рис.3.2. В этом случае конденсаторы на участках MAN и MBN соединены последовательно, а сами участки соединены параллельно. Определим электроёмкости участков MAN и MBN, они равны между собой и определяются согласно (3.6):
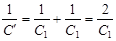 .
.
Отсюда получим:
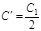 . (3.10)
. (3.10)
Для параллельно соединенных участков с электроёмкостями  , используя (3.5) и (3.10) получим:
, используя (3.5) и (3.10) получим:
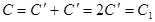
Ответ: С=С 1.
Задача 9. Пространство между обкладками конденсатора частично заполнено диэлектриком с диэлектрической проницаемостью 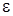 . Площадь пластины равна S. Найдите электроёмкость конденсатора для случаев, показанных на рис. 3.3 а, б.
. Площадь пластины равна S. Найдите электроёмкость конденсатора для случаев, показанных на рис. 3.3 а, б.
| Дано: ε S L d l h | Решение.
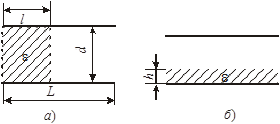 Рис. 3.3
Рис. 3.3
|
| С -? |
Физическая система состоит из конденсатора, частично заполненного диэлектриком. Рассмотрим случай, показанный на рис. 3.3-а. Данный конденсатор можно рассматривать как систему двух параллельно соединенных конденсаторов с электроемкостью С1 и С2 (см рис 3.4). Для параллельного соединения конденсаторов электроемкость определяется выражением (3.5)

Рис 3.4
Определим С 1 и С 2 в соответствии с (3.3)
 , (3.11)
, (3.11)
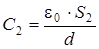 , (3.12)
, (3.12)
здесь S1 - площадь обкладок конденсатора С1, S2 - площадь обкладок конденсатора С2.
По условиям задачи на рис 3.3.а площадь обкладок равна S=Lb, где b – ширина пластин, b=S/L. Найдем S 1 и S 2:
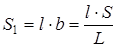 , (3.13)
, (3.13)
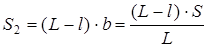 (3.14)
(3.14)
Подставим (3.13) и (3.14) в (3.11) и (3.12)
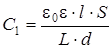 (3.15)
(3.15)
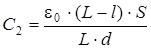 (3.16)
(3.16)
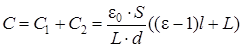
В случае, показанном на рис 3.3.б, конденсатор можно рассматривать как систему двух последовательно соединенных конденсаторов (см. рис 3.5) с электроемкостями С 3 и С 4:
 Рис 3.5
Рис 3.5
| 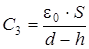
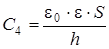
| (3.17) (3.18) |
При последовательном соединении (3.6) электроемкость батареи находится из выражения:
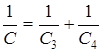 (3.19)
(3.19)
Из (3.19) с учетом (3.17) и (3.18) получим:
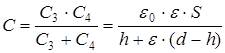
Ответ: а) 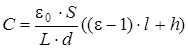 ; б)
; б) 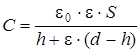 .
.
Задача 10. Конденсатор электроёмкостью С 1 =3мкФ был заряжен до разности потенциалов U 1 =40В. После отключения от источника тока конденсатор был соединен параллельно с другим конденсатором Электроёмкостью С 2 =5мкФ. Определить энергию 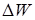 , израсходованную на образование искры в момент присоединения второго конденсатора.
, израсходованную на образование искры в момент присоединения второго конденсатора.
| Дано: С 1 = 3 мкФ C 2 = 5 мкФ U 1 = 40 B |
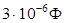

| Решение.
Физическая система состоит из двух конденсаторов. Из закона сохранения энергии следует, что энергия, израсходованная на образование искры равна:
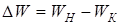 , (3.34)
где WН – начальная энергия физической системы, WК – , (3.34)
где WН – начальная энергия физической системы, WК –
|
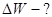
|
конечная энергия этой системы после образования искры.
Начальная энергия – это энергия заряженного конденсатора  из (3.7):
из (3.7):
 . (3.35)
. (3.35)
После соединения конденсаторов в батарею энергия системы будет равна:
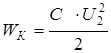 . (3.36)
. (3.36)
где 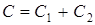 (см. (3.5)) – электроемкость батареи,
(см. (3.5)) – электроемкость батареи, 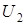 - напряжение на батарее.
- напряжение на батарее.
С учетом (3.35), (3.36) и (3.34) получим:
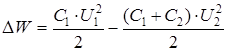 (3.37)
(3.37)
Из закона сохранения заряда следует, что после присоединения второго конденсатора заряд остался прежним. Выразим разность потенциалов 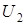 из (3.2):
из (3.2):
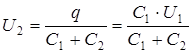 . (3.38)
. (3.38)
Подставим (3.38) в (3.37):
 ,
,
или после преобразований:
 (3.39)
(3.39)
Подставим в (3.39) числовые значения:
|
|
