
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
I. 3. Напряженность поля точечного заряда в вакууме
|
|
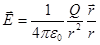
I. 4. Принцип суперпозиции электростатических полей.
Результирующая сила  , действующая со стороны поля на пробный заряд Q0, равна векторной сумме сил
, действующая со стороны поля на пробный заряд Q0, равна векторной сумме сил  , приложенных к нему со стороны каждого из зарядов Qi :
, приложенных к нему со стороны каждого из зарядов Qi :
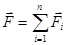
Где  и
и 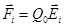 , где
, где 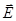 – напряженность результирующего поля, а
– напряженность результирующего поля, а 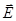 i – напряженность поля, создаваемого зарядом Qi., получаем
i – напряженность поля, создаваемого зарядом Qi., получаем
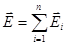
Формула (1.5) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность 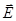 результирующего поля, создаваемая системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
результирующего поля, создаваемая системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
На рис. 1.5 приведен пример суперпозиции вектора 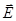 для двух зарядов q1 и q2 в точках А и С.
для двух зарядов q1 и q2 в точках А и С.
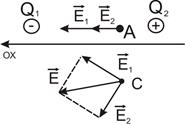
Рис. 1.5
I. 5. Электрический момент диполя или дипольным момент.
Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя 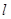 . Вектор
. Вектор
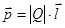
совпадающий по направлению с плечом диполя и равный произведению заряда  на плечо
на плечо 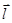 , называется электрическим моментом диполя или дипольным моментом.
, называется электрическим моментом диполя или дипольным моментом.
Электрический диполь – система двух равных по модулю разноименных точечных зарядов (+Q, -Q), расстояние 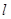 между которыми значительно меньше расстояния до рассматриваемых точек поля (рис. 1.6).
между которыми значительно меньше расстояния до рассматриваемых точек поля (рис. 1.6).

Рис. 1.6

ОХ: 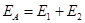
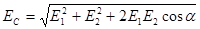
I. 6. Поток вектора напряженности электростатического поля.
Число линий напряженности, пронизывающих элементарную площадку dS, нормаль  к которой образует угол
к которой образует угол 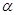 с вектором
с вектором 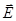 , равно
, равно  , где Еn – проекция вектора Е на нормаль
, где Еn – проекция вектора Е на нормаль  к площадке
к площадке 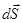 (рис. 1.7). Величина
(рис. 1.7). Величина
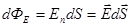

Рис. 1.7
называется потоком вектора напряженности через площадку 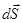 ,
,
где 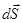 =dS
=dS  – вектор, модуль которого равен dS, а направление совпадает с направлением нормали
– вектор, модуль которого равен dS, а направление совпадает с направлением нормали  к площадке. Выбор направления вектора
к площадке. Выбор направления вектора  (а следовательно, и dS) условен, так как его можно направить в любую сторону. Единица потока вектора напряженности электростатического поля –
(а следовательно, и dS) условен, так как его можно направить в любую сторону. Единица потока вектора напряженности электростатического поля – 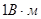 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Для произвольной замкнутой поверхности S поток вектора 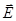 сквозь эту поверхность
сквозь эту поверхность
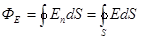
где интеграл берется по замкнутой поверхности S. Поток вектора 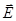 является алгебраической величиной: зависит не только от конфигурации поля Е, но и от выбора направления
является алгебраической величиной: зависит не только от конфигурации поля Е, но и от выбора направления  . Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т. е. нормаль, направленная наружу области, охватываемой поверхностью.
. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т. е. нормаль, направленная наружу области, охватываемой поверхностью.
I. 7. Теорема Гаусса для электростатического поля.
Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на  .
.
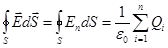
В общем случае электрические заряды могут быть «размазаны» с некоторой объемной плотностью  , различной в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, охватывающий некоторый объем V,
, различной в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, охватывающий некоторый объем V,

Теорему Гаусса (1.13) можно записать так:

|
|
