Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Узловым потенциалом называется потенциал узла сложной цепи относительно узла, потенциал которого принят равным нулю.

Размечаем произвольно потенциалы узлов 1 и 2 и токи в ветвях цепи.

По первому закону Кирхгофа для незаземленных узлов будем иметь

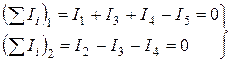. (1.70)

Токи в ветвях определяются по закону Ома:

;

;

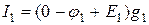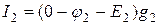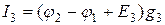; (1.71)

;

,

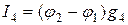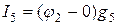где

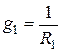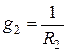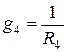; ; ; ; - проводимости ветвей.

Подставляя (1.71) в (1.70), будем иметь:

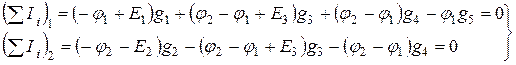; (1.72)

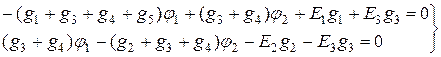. (1.73)

Введем обозначения:

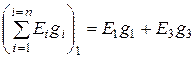(1.74)

- алгебраическая сумма произведений ЭДС на соответствующие проводимости, примыкающие к узлу 1 цепи;

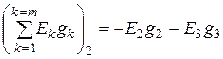(1.75)

- то же, но примыкающая к узлу 2 цепи.

Произведение ЭДС на проводимость берут со знаком плюс, если стрелка ЭДС источника направлена к рассматриваемому узлу и минус, если она направлена от узла.

Сумма проводимостей ветвей, присоединенных к узлам 1 и 2, запишется так:

;

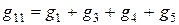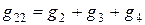. (1.76)

Величины 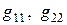- называют проводимостями узлов.

Сумма проводимостей ветвей, соединяющих узлы 1 и 2, записывается так:

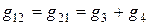. (1.77)

В дальнейшем будем называть 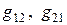- проводимостями между узлами.

Подставим (1.74), (1.75), (1.76), (1.77) в (1.73):

;

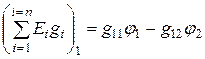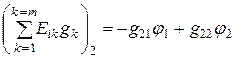. (1.78)

Если в цепи действует не только ЭДС, но и источник тока, то эти токи следует учесть в левых частях уравнений (1.78).

Токи «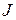» заданных источников тока записываются в левые части уравнений со знаком плюс, если они притекают к узлу и со знаком минус, если они вытекают из узла.

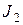Положим, что притекает к узлу 1, а вытекает из узла 2.

В результате получим:

;

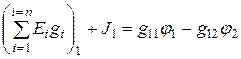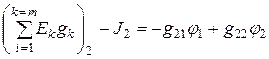. (1.79)

Если электрическая цепь имеет в своем составе 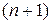узлов ( 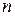- любое число), то положив потенциал, например 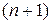узла, равным нулю для определения остальных 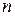потенциалов, получим систему из 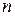уравнений.

. (1.80)

Решая систему (1.80) относительно определяем потенциалы узлов, а затем по формулам типа (1.71) находим токи в ветвях цепи.

Применим изложенный метод к сложной цепи, изображенной на рисунке 1.36.

Для цепи, изображенной на рисунке 1.32, дано: Е ₁; Е ₄; R ₁; R ₂; R ₃; R ₄; R ₅; R ₆.

Найти

1. Все токи.

2. Проверить полученные результаты на баланс токов и баланс мощности.

3. Напряжения на всех элементах цепи.

Рисунок 1.32 - Расчетная схема

Порядок расчета

1. Заземляем один из узлов цепи.

Заземлению можно подвергнуть любой из четырех узлов цепи. Обозначаем потенциал заземленного узла через «0».

2. Размечаем цифрами незаземленные узлы.

Разметку узлов можно производить в произвольном порядке.

3. Размечаем потенциалы незаземленных узлов.

На схеме это - .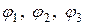

4. Определяем проводимости всех ветвей цепи:

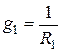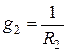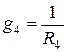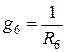; ; ; ; ; . (1.81)

5. Составляем уравнения узловых потенциалов.

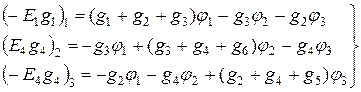. (1.82)

Примечание:

Если в цепи имеется ветвь с ЭДС (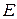) не содержащая сопротивления, то именно узел такой ветви следует заземлять. Заземленный узел имеет при это потенциал равный нулю, тогда другой узел и его потенциал найдется без расчета 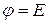. Число расчетных уравнений уменьшается на единицу.

6. Решаем систему уравнений узловых потенциалов.

Решение производим методом определителей, или используя вычислительную технику:

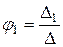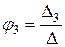; ; . (1.83)

7. Размечаем стрелки действительных токов на ветвях цепи.

Стрелки токов можно размечать как обычно, то есть произвольно.

8. Определяем величины действительных токов в ветвях цепи.

Для определения токов используем значения ранее вычисленных потенциалов узлов и закон Ома:

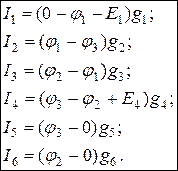. (1.84)

9. Поверяем действительные токи на баланс токов

Проверку производим во всех независимых узлах цепи по первому закону Кирхгофу.

10. Проверяем действительные токи на баланс мощности

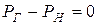. (1.85)