Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Метод линейных преобразований

Данный метод основан на использовании закона Ома и формул последовательного, параллельного, смешанного соединения соп­ротивлений, а также перехода от соединения сопротивлений в треугольник к звезде.

Сначала сложная цепь свертывается до предельно простой и решается по закону Ома – прямой путь. Затем, полученное решение развертывается до заданной конфигурации цепи – обратный путь. Основное условие применимости метода – в цепи должен быть только один источник пи­тания.

Дано: цепь, показанная на рисунке 1.24; параметры Е, R ₁, R ₂, R ₃, R ₄, R ₅, R ₆.

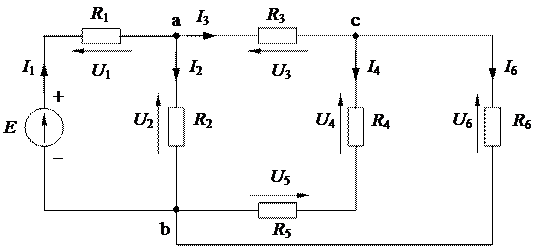Рисунок 1.24 – Исходная схема цепи

Найти

1. Эквивалентное сопротивление всей цепи относительно зажимов источника питания.

2. Все токи.

3. Проверить полученные результаты на: а) баланс токов, б) баланс мощности.

4. Напряжения на всех элементах цепи.

5. Проверить напряжения на баланс напряжений.

Порядок расчета

1. Расставляем на исходной схеме стрелки токов.

Поскольку в схеме только один источник энергии токи можно разметить сразу в правильном направлении. Токов будет столько, сколько ветвей в цепи. Стрелки токов размечают непосредственно на проводниках.

2. Размечаем стрелки напряжений. Напряжения расставляются на каждом элементе цепи. Направление стрелок напряжений всегда выбирается против токов текущих в ветви.

3. Определяем эквивалентное сопротивление всей цепи относительно зажимов источника питания.

Свертываем цепь (прямой путь). Первое преобразование (показано на рисунке 1.25).

Рисунок 1.25 – Расчетная схема после первого преобразования

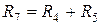. (1.39)

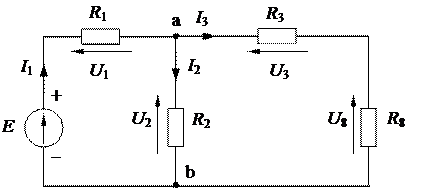Проводим второе преобразование цепи (схема показана на рисунке 1.26).

Рисунок 1.26 – Расчетная схема после второго преобразования

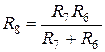. (1.40)

Третье преобразование (см. рисунок 1.27).

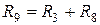. (1.41)

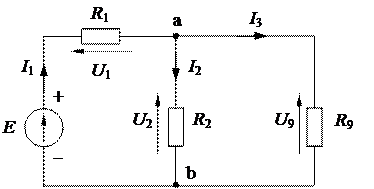
Рисунок 1.27 – Расчетная схема после третьего преобразования

Четвертое преобразование (см. рисунок 1.28).

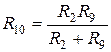. (1.42)

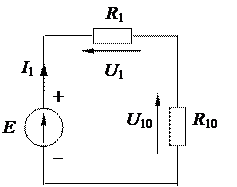Рисунок 1.29 – Расчетная схема после четвертого преобразования

Последнее, пятое преобразование (см. рисунок 1.30).

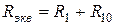. (1.43)

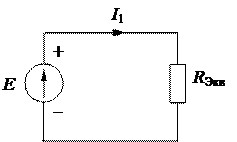
Рисунок 1.30 – Расчетная схема после пятого преобразования

Определяем ток 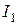, в схеме на рисунке 1.30, по закону Ома.

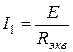. (1.44)

4. Развертываем решение (обратный путь) и находим токи в ветвях цепи. Воспользовавшись схемой изображенной на рисунке 1.27, найдем ток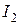и и :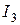

;

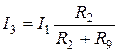. (1.45)

Переходя к рисунку 1.25, определяем ток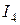и и :

;

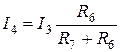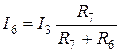. (1.46)

Ток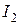и , и можно найти по-другому, например из рисунка 1.27:

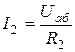; . (1.47)

Согласно второму закона Кирхгофа имеем

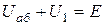, откуда

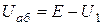, напряжение 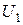определится по закону Ома

.

5. Проверка полученных результатов.

а) Баланс токов.

Из рисунка 1.25 следует:

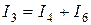; (1.48)

,

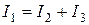б) Баланс мощности.

Мощность вырабатываемая генератором

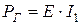. (1.49)

Мощность нагрузки

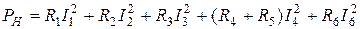. (1.50)

6. Определяем напряжения на всех участках цепи. Делаем это по закону Ома:

;

;

;

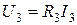; (1.52)

;

.

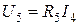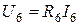7. Проверяем напряжения на баланс напряжений. Для этого, составим урав­нения по второму закону Кирхгофа для цепи изображенной на рисунке 1.25.

Первое уравнение

. (1.53)

Второе уравнение

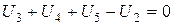. (1.54)

Третье уравнение

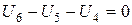или . (1.55)

Если балансы тока, напряжения и мощности сошлись с погрешностью не более 1%, то расчет считается выполненным правильно.