Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод теоремы Поливанова
|
|
Метод теоремы К. М. Поливанова так же, как и метод эквивалентного генератора позволяет определять только один ток в сложной цепи.
В противоположность теореме Тевенена-Гельмгольца здесь используется не режим холостого хода, а режим короткого замыкания ветви, в которой отыскивается ток.
Рассмотрим теорию данного метода.
Согласно теореме об эквивалентном генераторе (см. рисунок 1.35) имеем
| Рисунок 1.39 - К методу Поливанова |
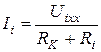. (1.93)
Разделим числитель и знаменатель выражения (1.93) на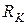 
, тогда получим
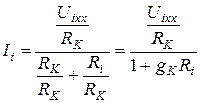. (1.94)
Числитель выражения (1.94) представляет собой ток короткого замыкания эквивалентного генератора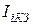 
в i - й ветви, см. рисунок 1.39, который определяется так
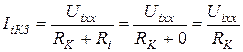. (1.95)
Подставляя (1.95) в (1.94) получим
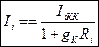, (1.96)
где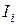 
- искомый ток в i - й ветви; 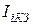- ток короткого замыкания в i - й ветви, то есть ветви в которой отыскивается ток; 
- проводимость всей цепи, замеренная с клемм i - й ветви; 
- сопротивление i - й ветви.
Выражение (1.96) называется теоремой Поливанова.
Рассмотрим применение теоремы Поливанова к отысканию тока в сложной цепи.
Для цепи, изображенной на рисунке 1.40, дано: Е 1; Е 3; R 1; R 2; R 3.
Найти - ток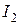 
, методом Поливанова.
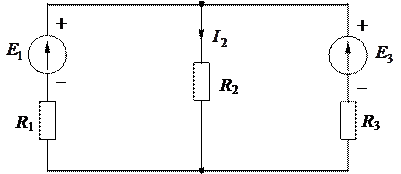
Рисунок 1.40 - Исходная схема
Порядок расчета
1. Составляем расчетную схему для отыскания тока короткого замыкания во второй ветви, (рисунок 1.41).
| Рисунок 1.41 - Режим холостого хода |
Для этого, закорачиваем сопротивление второй ветви.
Если ветвь активная, то закорачиванию подлежит только сопротивления, а источник энергии в ветви должен быть оставлен.
2. Определим величину тока короткого замыкания во второй ветви.
Расчет производится по расчетной схеме любыми методами, дающими самое короткое решение.
В нашем случае имеем
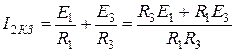. (1.97)
3. Составляем расчетную схему для определения проводимости цепи .
Рисунок 1.42 - Режим короткого замыкания |
При составлении схемы все ЭДС источников полагают равными нулю, внутренние сопротивления источников оставляют в схеме. Схема показана на рисунке 1.42.
4. Определяем величину ,
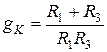. (1.98)
5. Определяем величину тока .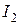
Для этого записываем теорему Поливанова
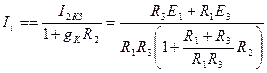. (1.99)
Метод широко применяется на практике.
|
|