Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Виды движения точки в зависимости от ускорения

В зависимости от ускорения выделяю четыре вида движения точки.

1. Равномерное и прямолинейное движение точки.

При этом движении скорость движения точки А постоянна, а радиус кривизны траектории движения точки А = ∞ (рис. 1.32).

В этом случае касательное ускорение a _τ = 0, так как

(V = const), нормальное ускорение a_n = 0, так как (р = ∞).

Следовательно, полное ускорение движения точки a = 0.

2. Равномерное криволинейное движение.

При этом движении величина скорости движения точки А постоянная (V = const), изменяется лишь направление скорости, при этом величины радиусов кривизны траектории точки имеют конечные значения (рис. 1.33).

В этом случае имеем следующее:

касательное ускорение a _τ = 0, так как (V = const)

нормальное ускорение a_n ≠ 0, так как 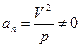(ρ – конечная вели-

чина).

Следовательно, полное ускорение при равномерном криволинейном движении состоит только из нормального ускорения:

= .

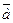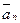3. Неравномерное прямолинейное движение.

При этом движении величина скорости движения точки V = f (t), а радиус кривизны траектории точки ρ = ∞.

В этом случае касательное ускорение a _τ ≠ 0, так как

нормальное ускорение a_n = 0, так как , (ρ = ∞).

Следовательно, полное ускорение точки при неравномерном прямолинейном движении состоит только из касательного ускорения:

= .

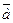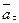4. Неравномерное криволинейное движение.

При этом движении величина скорости движения точки V = f (t), а радиус кривизны траектории точки ρ ≠ ∞, т.е. является конечной величиной.

В этом случае касательное ускорение a _τ ≠ 0, так как

нормальное ускорение an ≠ 0, так как 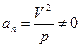, 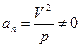(ρ – конечная величина).

Полное ускорение точки при неравномерном криволинейном движении складывается геометрически из касательного и нормального ускорений:

= +

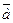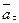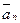
Равномерно-переменное движение точки. В том случае, когда величина касательного ускорения постоянна, т.е. a _τ = const, движение точки называется равномерно-переменным.

Если абсолютная величина скорости уменьшается, то такое движение называется равнозамедленным.

Запишем формулу для определения касательного ускорения:

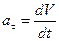или dV = a_τ ⋅ dt.

Проинтегрируем это уравнение:

V = ∫ a _τ ∙ dt,

так как a _τ = const, то

V = a _τ ∫ dt = a _τ ∙ t + V ₀,

где V ₀ − постоянная интегрирования, характеризующая начальную скорость точки.

При равномерно-ускоренном движении a _τ > 0, при равномерно замедленном a _τ < 0.

Касательное ускорение определится как

Если начальная скорость точки V ₀ равна нулю, то .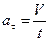

Учитывая, что скорость можно определить как 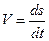, имеем выражение

dS = (a _τ ∙ t + V ₀) dt.

Проинтегрировав это уравнение с учетом того, что a _τ = const и V ₀ = const, получим формулу для определения расстояния точки от начала отчета в равномерном движении для любого момента времени

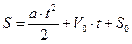, (1.19)

где S ₀ − постоянная интегрирования, характеризующая начальное положение точки.

При S ₀ = 0 формула (1.19) примет вид

С учетом формулы V = a _τ ∫ dt = a _τ ∙ t + V ₀ получим выражение для определения пути в виде .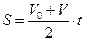

П р и м е р. По дуге радиуса R, равномерно-замедленно двигается поезд, его скорость в начальном движении по дуге составила V ₀ =15 м/с. После того, как поезд прошел расстояние S = 500 м, его скорость уменьшилась до V =10 м/с. Определить полное ускорение в начале и конце движения.

1. 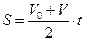. Отсюда определим время t:

.

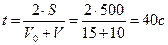2. Определим касательное ускорение a _τ :

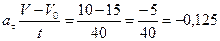м/с²

a _τ = const в течение всего времени движения.

3. Найдем нормальное ускорение:

в начале движения оно равно м/с²

в конце пути – 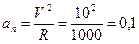м/с²

4. Величины полных ускорений равны:

в начале движения

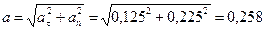м/с²

в конце пути

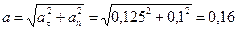м/с²