
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Момент силы относительно оси
|
|
На твердое тело действует сила F, приложенная в точке A (рис. 1.28). Необходимо определить момент этой силы относительно оси z.
Проведем через точку A плоскость xy, перпендикулярную оси z, и разложенную силу F на составляющие – Fz, параллельную оси z и Fxy, перпендикулярную оси z.

| Рис. 1.28. Схема к определению момента силы |
Сила Fz направленная параллельно оси z не может повернуть тело вокруг оси z, т.е. вращать тело вокруг оси z будет только сила Fxy:
mz (F) = mz (Fxy),
mz (F) = ± Fxy ∙ h.
Моментом силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, который взят относительно точки пересечения оси с плоскостью.
Правило знаков. Если при взгляде с положительного конца оси сила стремится повернуть тело против хода часовой стрелки, то момент положительный, если по ходу часовой стрелки, то момент отрицательный.
При вычислении моментов нужно помнить следующие частные случаи:
1.Если сила параллельна оси, то ее момент равен нулю, так как Fxy = 0.
2.Если линия действия силы пересекает ось, то ее момент равен нулю, так как h = 0.
Вывод. Момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
3. Если сила перпендикулярна к оси, то mz = 0.
Рассмотрим аналитические выражения для моментов силы относительно осей координат.
Спроектируем силу F сначала на плоскость, xy перпендикулярную оси z, а затем на оси x и y (рис. 1.29).
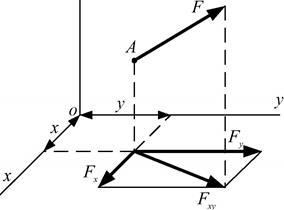
| Рис. 1.29. Схема к определению моментов сил относительно осей координат |
Из теоремы Вариньона очевидно, что
mz (F) = mO (Fxy) = mO (Fx) + mO (Fy),
mz (F) = Fy ∙ x − Fx ∙ y.
Аналогично можно записать выражения моментов относительно других осей:
mx (F) = Fz ∙ x − Fy ∙ y,
my (F) = Fx ∙ x − Fz ∙ y,
mz (F) = Fy ∙ x − Fx ∙ y.
Условия равновесия произвольной пространственной системы сил.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно осей были равны нулю:
Σ Fnx = 0, Σ Fny = 0, Σ Fnz = 0,
Σ mx (Fn) = 0, Σ my (Fn) = 0, Σ mz (Fn) = 0.
Для случая параллельных сил остаются три условия равновесия, т.к остальные три обращаются в тождество 0 = 0:
Σ Fnz = 0, Σ mx (Fn) = 0, Σ my (Fn) = 0.
|
|
