
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Распределение судейских оценок суждения
|
|
(описание поведения суждения)
| Градации | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) |
| Числовые значения | |||||||||||
| Относительная частота | |||||||||||
| Накопленная частота (кумулятивный процент) |
Примечание. Относительная частота – процент судей, отнесших суждение к данной градации. Экспертов – 100. Здесь показаны данные по одному суждению.
Третий этап. На данном этапе рассматривается поведение каждого суждения, т.е. определяется, какое количество экспертов отнесли суждение к той или иной градации. Суждению, помещенному в ячейку, тем самым приписывается число (оценка), которое позволяет определить степень единодушия экспертов по отношению к выбранным суждениям.
Градацию принимаем за балл, который эксперт дает тому или иному суждению.
Другими словами, на этом этапе определяется:
а) " цена" каждого суждения на шкале в 11 интервалов;
б) степень согласованности решений экспертов.
Из табл. 13 видно, что во второй строке даны абсолютные цифры, а в третьей показана доля (в процентах) экспертов, отнесших суждение в соответствующую градацию (относительная частота). Например, 1% экспертов отнесли суждение к первой градации, 4 % – ко второй градации, 2 % – к третей, 3 % – к четвертой и т.д. Последняя строка показывает накопленную частоту или кумулятивную частоту. Она показывает распределение процентов по нарастающей от 0 до 100. Накопленная частота означает, что 7 % экспертов дали суждению 3 балла и меньше, а 43 % дали 6 баллов и меньше.
95 % экспертов дали суждению балл 9 и меньше 9, а 96 % показывает, что такое количество экспертов дали суждению балл, равный 10 и меньше. 100 % экспертов дали суждению балл 11 и меньше.
Распределение кумулятивных (накопленных) процентов позволяет вычислить значения медианы и междуквартильного размаха.
Медиана – это величина признака, находящаяся в середине ранжированного ряда. Медиана делит пополам упорядоченное множество значений признака.
В данном случае медиана означает, что 50 % дают оценку меньше этого балла, а 50 % – больше.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Медиана или процентиль 50 в распределении накопленных частот – это такое значение на шкале градаций (1–11), относительно которого половина судей дала большие, а другая половина – меньшие оценки данного утверждения.
Вычислить медиану мы можем по формуле или графически
Me = Xо + dХ ´ 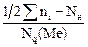 ,
,
где Xо – нижняя граница интервала медианы (нижнего или верхнего квартилей); dХ – величина интервала; Nн – накопленная частота (частость) до нижней границы интервала (медианы, квартиля); Nq – относительная частота интервала (медианы, квартиля); Sni – сумма частот (частостей) интервала.
Mе =  .
.
В нашем случае:
Нижняя граница интервала медианы – 6, 5.
Ширина интервала – 1.
Накопленная частота до нижней границы интервала медианы (кумулятивный процент) – 43.
Относительная частота интервала медианы (процент верхней границы интервала) – 30.
Далее следует посмотреть, в каком интервале вокруг медианы сосредоточены оценки 50 % респондентов (экспертов), т.е. какова степень единодушия экспертов по поводу данного суждения.
В методе Терстоуна ширина интервала между соседними численными градациями по определению равна 1 (равнокажущиеся интервалы). В используемом нами примере границами интервала, где расположена медиана (процентиль 50), являются градации 6 и 7 (см. табл. 2), т.е. делим пополам сумму мест 6 и 7, получаем значение нижней границей интервала медианы. Оно будет равно 6, 5.
Mе = 6, 5 + 1 ´ 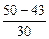 = 6, 7.
= 6, 7.
Значение медианы принимается за шкальный балл (" цену") суждения. В нашем примере он оказался равен 6, 7.
Не все суждения, получившие оценку " судей", в равной мере пригодны для шкалы: некоторые из суждений получат весьма согласованные и единодушные оценки экспертов, тогда как другие вызовут разнобой во мнениях.
Для оценки внутренней согласованности отдельных суждений определяется разброс судейских оценок. В качестве меры разброса используется квартильный размах, равный (Q3 – Q1), т.е. расстоянию (разнице) между первым и третьим квартилем распределения. В пределах квартильного размаха, т.е. вокруг медианы сосредоточены оценки 50 % респондентов.
Квартили обозначаются буквами Q1, Q2, Q3.
Q1 – такое значение признака, что одна четвертая часть всех объектов имеет значения, меньшие него, а три четверти – значения, большие него. Первый квартиль (Q1) задается точкой на оси, до которой лежит 25% полученных оценок суждения.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Q2 – такое значение, что половина всех объектов имеет значения, меньшие него, а – половина большие. Второй квартиль называют медианой и обозначают как Ме.
Q3 – означает точку, ниже которой находится 75 % оценок, а выше лежит 25% оценок.
Для вычисления междуквартильного размаха (Q3 – Q1) сначала устанавливаются значения, соответствующие первому и третьему квартилям распределения. Для этого используются формулы, аналогичные формуле для медианы, с соответствующими поправками: берется фактическая нижняя граница интервала соответствующего квартиля, кумулятивный процент для нижней границы интервала данного квартиля и т.д. Так, для первого квартиля формула подсчета такова:
Q1 = Xо + dХ ´ 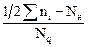 .
.
Q1 = 
Для нашего примера:
Q1 = 5, 5 + 1 ´ 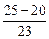 = 5, 7.
= 5, 7.
Для третьего квартиля (75 процентиль) произвести необходимые подсчеты можно по такой же формуле, только беря цифры вокруг относительной накопленной частоты 75 %.
Q3 = 7, 5 + 1 ´ 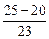 = 7, 6.
= 7, 6.
| 100 % |

| Q1 | Q2 = Ме | Q3 |
Рис. 8
Междуквартильный размах составит
(Q 3 – Q 1) = 7, 6 – 5, 7 = 1, 9.
Есть графический метод нахождения медианы, квартилей. Для этого строится кривая накопленных процентов – кумулята, позволяющая легко найти числовое значение, соответствующее 25, 50 и 75 % (рис. 8).
Кумулята – график накопленных частот. По горизонтали откладываем градации на шкале, а по вертикали – накопленную частоту, т.е. по оси абсцисс мы показываем границы интервалов (либо значения дискретного признака), а на оси ординат – накопленные частоты (либо относительные частоты), соответствующие верхним границам интервалов.
Кумулята позволяет определить процент респондентов, находящихся ниже или выше заданной величины признака (рис. 9).

Рис. 9. Кумулята
Степень единогласия экспертов определяется по квартильному отклонению: Q = 1/2 (Q3 – Q1).
В результате анализа поведения всех суждений по каждому суждению мы получаем медиану и квартильный размах.
Теперь можем около каждой градации исходной шкалы образовать группу суждений, у которых медианы почти одинаковы, т.е. группировать градации. Таких групп может быть девять или 11.
Четвертый этап. Этап отбора качественных суждений в шкалу, в анкету и построения собственно установочной шкалы, которая позволит каждому респонденту найти значение, отвечающее его установке.
Сначала выбирают суждения со значением медианы около 1 и сравнивают их квартильные размахи. Суждения с большим квартильным размахом отбрасывают, а с минимальным – включаем в шкалу. Чем меньше квартильный размах, тем лучше суждение, так как по ним мнения экспертов более согласованы, их оценки достаточно единодушны. Такие суждения могут более точно отражать позицию респондентов. (Если необходимо обеспечить большую точность шкальных значений каждого высказывания, то можно провести вторую стадию строгой оценки суждений с использованием метода парных сравнений.)
При отборе суждений может возникнуть ситуация, когда в группе есть одно суждение, к тому же с большим квартильным размахом. Нужно выяснить, почему низка степень единодушия экспертов по этому суждению и почему нет других суждений в этой группе?
Нужно сделать так, чтобы суждения равномерно покрывали исходную шкалу. Это значит, что как минимум нужно отобрать 9 или 11 суждений (в нашем случае), из каждой кучки по суждению.
В окончательном виде шкала может содержать от 15 до 30 суждений, каждое из которых имеет свой вес.
После этих этапов шкала готова для использования. Проводится пилотаж с последующей доработкой шкалы. С ее помощью мы будем измерять социальные установки респондентов.
Как измерить установку респондента?
Составляется список из оставленных суждений, и включают их в анкету для опроса основной массы респондентов. Причем суждения даются в случайном порядке, они вставляются в различные места анкеты, вразнобой, их веса являются неизвестными для респондентов. Респонденту предлагают отметить то суждение, с которым он согласен. Затем выписываем значения медианы тех суждений, с которыми респондент согласился. Упорядочиваем эти значения в порядке возрастания или убывания. Затем находим среднюю тенденцию (медиану), т.е. мы ищем медиану из медиан, которая и есть значение установки респондента. Это среднее и будет шкальным значением респондента, результатом измерения его установки.
Например, в ответах респондента имеется 4 принятых суждения с весами 4, 4; 4, 8; 5, 6; 6, 1. Тогда ранг респондента будет соответствовать его медиане 5, 1. При четном числе принятых пунктов медианный ранг можно принять как среднеарифметическое интервала, в котором лежит медиана.
Если полученную шкалу предъявить теперь группе респондентов, то индивидуальным баллом каждого субъекта, выражающим меру " благожелательности" его установки, можно считать медиану (или средний балл) всех суждений, с которыми он согласился.
Ранговая позиция группы опрошенных определяется как среднеарифметическое рангов всей совокупности, составляющей группу.
Практика показывает, что не обязательно нужно составлять такое большое количество суждений на первом этапе, как это предлагал Терстоун.
Также не обязательно вовлекать такое большое число экспертов, можно получить устойчивые данные с использованием труда 20–30–50 экспертов.
За счет снижения дробности шкалы повышается надежность, но снижается точность замера. Если предлагать судьям раскладывать суждения не в 11, а в 5 ячеек (интервалов), то итоговая шкала будет более надежной, но менее точной.
Выбор в пользу большей-меньшей точности зависит от предмета исследования и значимости гипотез, а также от того, насколько точно измеряются в нем другие переменные. Если большинство переменных измеряется по трехчленным и пятичленным шкалам, то только одна – по 11-членной, и притом все переменные подлежат взаимной корреляции, в этом случае использовать 11-членную шкалу вряд ли оправданно.
|
|
