Иерархические системы распознавания

При распознавании сложных объектов (слов устной речи; названий городов, рек, озёр и пр. на географических картах; составных изображений, являющихся комбинацией неких геометрических примитивов) целесообразно использовать иерархические распознающие процедуры. В какой-то мере мы касались этого подхода при рассмотрении лингвистических (структурных) методов распознавания. Как следует из самого названия, особенностью иерархических распознающих процедур является их многоуровневость. На нижнем уровне распознаются элементарные образы (примити­вы), на более высоких уровнях – составные образы. Естественно, число уровней может быть различным. Мы для определённости будем рассматривать двухуровневую систему распознавания.

Можно выделить два вида двухуровневой системы распознавания. Первый характеризуется наличием естественной временной или пространственной последовательности образов первого уровня, поступающей для распознавания на второй уровень. Например, это может быть последовательность фонем при распознавании устных слов или последовательность букв при распознавании названий на географической карте. Здесь структурные связи между образами первого уровня предельно упрощены и описываются порядком следования. Во втором виде двухуровневых систем распознавания структурные связи между образами первого уровня более сложны. Например, если буквы распознаются двухуровневой системой, то образы первого уровня (отрезки прямых, дуг) связаны друг с другом на плоскости по некоторым правилам, более сложным, чем простое следование. Именно этот вариант мы рассмотрели ранее, когда речь шла о лингвистических методах распознавания.

В данном разделе мы остановимся на случае, когда на вторую ступень распознавания поступает естественная последовательность образов первого уровня.

Итак, на вторую ступень поступает не сам объект, а результаты распознавания его элементов на первой ступени 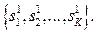Длина 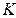таких последовательностей в общем случае различна. Алфавит образов второго уровня распознавания представляет собой множество последовательностей образов первого уровня и может быть существенно больше алфавита образов первого уровня. Например, из 32 букв русского алфавита могут состоять десятки тысяч распознаваемых слов.

Если бы распознавание образов на первом уровне было безошибочным, то распознавание на втором уровне сводилось бы к выбору из алфавита второго уровня той последовательности, которая совпала с последовательностью, полученной на выходе первого уровня распознающей системы. Однако на практике при распознавании неизбежны ошибки, в том числе и в иерархических системах, а в последних на различных уровнях распознавания. Если на первом уровне допущены ошибки, то на вход второго уровня может поступить последовательность, не совпадающая ни с одним из образов, входящих в алфавит второго уровня, тем не менее какое-то решение принимать необходимо. Возможен, например, такой детерминистский вариант. Из алфавита выбираются те последовательности, которые содержат столько же элементов, сколько их содержится в предъявляемой к распознаванию последовательности. Затем распознаваемая последовательность накладывается на отобранные из последовательности и подсчитывается число несовпадающих элементов. Отнесение к тому или иному образу осуществляется по минимуму числа несовпадающих элементов. Такой подход является в определённой мере аналогом ранее рассмотренного метода минимума расстояния до эталона, только метрики при этом используются различные.

Здесь мы полагали, что ошибки распознавания, допущенные на первом уровне, искажают лишь тот или иной элемент последовательности, не влияя на общее их число. На практике же (в частности, при распознавании устных слов) может искажаться и число элементов в последовательности: появляются лишние ложные элементы либо пропускаются объективно имеющиеся. На этот случай имеются достаточно эффективные алгоритмы распознавания, реализуемые на второй ступени иерархических систем. Их изучение выходит за рамки настоящего курса.

Рассмотрим статистический подход к распознаванию в двухуровневой иерархической системе (рис. 26). Пусть на первом уровне распознаются образы 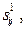где 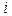– номер позиции в последовательности 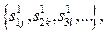выдаваемой первой ступенью для распознавания на вторую ступень; 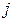– номер конкурирующего образа первой ступени на 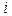-й позиции в последовательности.

Дело в том, что в иерархических распознающих системах целесообразно на промежуточных ступенях не принимать окончательное решение о принадлежности объекта к тому или иному образу, а выдавать набор вариантов с их апостериорными вероятностями. Этот набор должен быть таким, чтобы правильное решение входило в него с вероятностью, близкой к единице. Если все конкурирующие решения всех позиций считать вершинами графа, ввести формально начальную 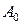и конечную вершины, соединить вершины дугами, как это показано на рис. 26, то получается ориентированный граф без циклов. Образу второго уровня распознавания соответствует вполне определённый путь в графе. На рис.26 помечен утолщёнными дугами путь, соответствующий последовательности 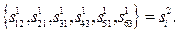В четвёртом столбце конкурирующих образов первой ступени имеется 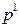– пустая вершина, соответствующая отсутствию элементов её столбца в последовательности. Наличие таких вершин позволяет удалять из последовательности " ложные " элементы, появившиеся в результате ошибок распознавания на первой ступени. Разумеется, при этом вершине 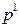должна быть соотнесена соответствующая апостериорная вероятность.

Рис. 26. Ориентированный граф, иллюстрирующий
процесс распознавания в двухступенчатой системе

На построенный граф " накладываются" образы (последова­тельности) из алфавита второй ступени, и тот из них, который имеет максимальную апостериорную вероятность 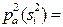, принимается в качестве решения на верхней ступени.

Здесь 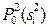– априорная вероятность образа 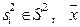– вектор параметров, характеризующих объекты на входе первой ступени распознавания.

Если говорить о последовательности букв, то каждая из них распознаётся независимо от других, поэтому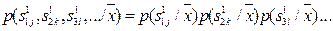

Описанная процедура применима в тех случаях, когда фиксирован алфавит 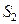. При обработке текстов это требование зачастую не выполняется. Так, например, дело обстоит при вводе текста со сканера и преобразовании изображения страницы с текстом в текстовый файл. Поскольку вводимые тексты имеют произвольное содержание, то зафиксировать словарь вряд ли возможно, да и нет в том особой необходимости. Ведь пользователю нужна лишь последовательность распознанных букв, знаков препинания и пробелов. Иными словами, можно было бы ограничиться только первой ступенью распознавания. Однако результаты такого распознавания требуют значительной редакторской правки, так как имеют место ошибки отнесения входных объектов к тому или иному образу. Например, при вероятности неправильного распознавания 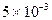на одну машинописную страницу текстового файла будет приходиться в среднем 10-12 грамматических ошибок. Весьма плачевный уровень грамотности. Его можно повысить хотя бы частичным моделированием второй ступени распознавания. Например, не имея фиксированного алфавита слов, можно зафиксировать алфавит двухбуквенных, трёхбуквенных и т.д. последовательностей. Количество таких последовательностей для каждого языка фиксировано, а их априорные вероятности (по крайней мере для двух букв) слабо зависят от словарного состава. На рис. 26 представлен граф, который можно использовать для двухбуквенных последовательностей. Использование большего числа букв ведёт к существенному усложнению графа без изменения принципа расчётов, поэтому мы ограничимся рассмотрением двухбуквенного варианта.

Если бы система распознавала слова, входящие в фиксированный алфавит , то записать априорную вероятность слова 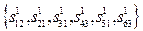можно было бы следующим образом:

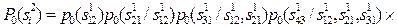
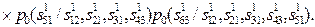
Если ограничиться использованием априорных вероятностей только двухбуквенных сочетаний, то

.

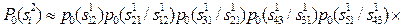
Вместо произведения можно оперировать суммой, если перейти от вероятностей к их логарифмам.

Итак, если каждой дуге приписать длину, равную 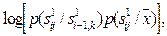то наиболее вероятной последовательности букв будет соответствовать путь максимальной длины на графе. Этот путь нетрудно найти методами, известными в теории графов.

Эффективность такого подхода для исправления ошибок первой ступени распознавания за счёт языковой избыточности подтверждена практическими испытаниями. Да это в некоторых случаях ясно и умозрительно. Например, при распознавании последовательности букв рассмотренный алгоритм уж точно обнаружит, а в большинстве случаев и исправит такие ошибки, как " гласная – твёрдый (мягкий) знак", " пробел – твёрдый (мягкий) знак", " мягкий знак – э" и ряд других.