
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Последовательные процедуры распознавания
|
|
Если в ранее рассмотренных методах распознавания принятие решения о принадлежности объекта тому или иному образу осуществлялось сразу по всей совокупности признаков, то в данном разделе мы обсудим случай последовательного их измерения и использования.
Пусть  . Сначала у объекта измеряется
. Сначала у объекта измеряется  и на основании этой информации решается вопрос об отнесении этого объекта к одному из образов. Если это можно сделать с достаточной степенью уверенности, то другие признаки не измеряются и процедура распознавания заканчивается. Если же такой уверенности нет, то измеряется признак
и на основании этой информации решается вопрос об отнесении этого объекта к одному из образов. Если это можно сделать с достаточной степенью уверенности, то другие признаки не измеряются и процедура распознавания заканчивается. Если же такой уверенности нет, то измеряется признак 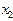 и решение принимается по двум признакам:
и решение принимается по двум признакам:  и
и 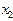 . Далее процедура либо прекращается, либо измеряется признак
. Далее процедура либо прекращается, либо измеряется признак 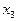 , и так до тех пор, пока либо будет принято решение об отнесении объекта к какому-либо образу, либо будут исчерпаны все
, и так до тех пор, пока либо будет принято решение об отнесении объекта к какому-либо образу, либо будут исчерпаны все  признаков.
признаков.
Такие процедуры чрезвычайно важны в тех случаях, когда измерение каждого из признаков требует существенных затрат ресурсов (материальных, временных и пр.).
Пусть  и известны
и известны 
 где
где 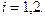 Заметим, что если известно распределение
Заметим, что если известно распределение 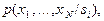 то известны и все распределения меньшей размерности (так называемые маргинальные распределения). Например,
то известны и все распределения меньшей размерности (так называемые маргинальные распределения). Например,


Пусть измерено 
 признаков. Строим отношение правдоподобия
признаков. Строим отношение правдоподобия  Если
Если 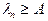 , то объект относим к образу
, то объект относим к образу 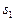 , если
, если 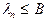 , то к образу
, то к образу 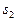 . Если же
. Если же 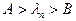 , то измеряется признак
, то измеряется признак 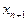 и вычисляется отношение правдоподобия
и вычисляется отношение правдоподобия  и т.д.
и т.д.
Понятно, что пороги  и
и  связаны с допустимыми вероятностями ошибок распознавания. Добиваясь выполнения неравенства
связаны с допустимыми вероятностями ошибок распознавания. Добиваясь выполнения неравенства 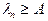 , мы стремимся к тому, чтобы вероятность правильного отнесения объекта первого образа к
, мы стремимся к тому, чтобы вероятность правильного отнесения объекта первого образа к 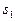 была в
была в  раз больше, чем ошибочное отнесение объекта второго образа к
раз больше, чем ошибочное отнесение объекта второго образа к 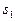 , то есть
, то есть 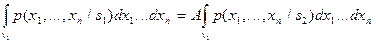 или
или 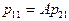 . Поскольку
. Поскольку  , то
, то 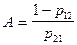 (верхний порог). Аналогичные рассуждения проводим для определения
(верхний порог). Аналогичные рассуждения проводим для определения  . Добиваясь выполнения неравенства
. Добиваясь выполнения неравенства 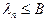 , мы стремимся к тому, чтобы вероятность правильного отнесения объекта второго образа к
, мы стремимся к тому, чтобы вероятность правильного отнесения объекта второго образа к 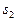 была в
была в 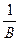 раз больше, чем неправильного отнесения объекта первого образа к
раз больше, чем неправильного отнесения объекта первого образа к 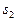 , то есть
, то есть
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
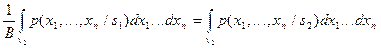 ,
,
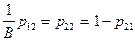 ,
,
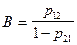 (нижний порог).
(нижний порог).
В последовательной процедуре измерения признаков очень полезным свойством этих признаков является их статистическая независимость. Тогда 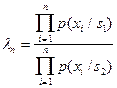 и нет необходимости в хранении (а главное – в построении) многомерных распределений. К тому же есть возможность оптимизировать порядок следования измеряемых признаков. Если их ранжировать в порядке убывания классификационной информативности (количество различительной информации) и последовательную процедуру организовать в соответствии с этой ранжировкой, можно уменьшить в среднем количество измеряемых признаков.
и нет необходимости в хранении (а главное – в построении) многомерных распределений. К тому же есть возможность оптимизировать порядок следования измеряемых признаков. Если их ранжировать в порядке убывания классификационной информативности (количество различительной информации) и последовательную процедуру организовать в соответствии с этой ранжировкой, можно уменьшить в среднем количество измеряемых признаков.
Мы рассмотрели случай с  (два образа). Если
(два образа). Если 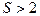 , то отношений правдоподобия может строиться
, то отношений правдоподобия может строиться 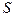 , например такого вида:
, например такого вида: 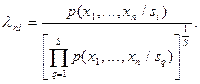 Останавливающая граница (порог) для
Останавливающая граница (порог) для  -го образа выбирается равной
-го образа выбирается равной 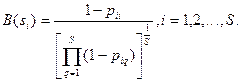 Если
Если 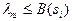 , то
, то  -й образ отбрасывается и строится
-й образ отбрасывается и строится  отношений правдоподобия и порогов
отношений правдоподобия и порогов  . Процедура продолжается до тех пор, пока останется неотвергнутым только один образ или будут исчерпаны все
. Процедура продолжается до тех пор, пока останется неотвергнутым только один образ или будут исчерпаны все 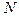 признаков. Если в последнем случае остались неотвергнутыми более чем один образ, решение принимается в пользу того из них, для которого отношение правдоподобия
признаков. Если в последнем случае остались неотвергнутыми более чем один образ, решение принимается в пользу того из них, для которого отношение правдоподобия  максимально.
максимально.
Если образов два ( ) и число признаков не ограничено, то последовательная процедура с вероятностью 1 заканчивается за конечное число шагов. Доказано также, что при заданных
) и число признаков не ограничено, то последовательная процедура с вероятностью 1 заканчивается за конечное число шагов. Доказано также, что при заданных 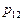 и
и  рассмотренная процедура при одинаковой информативности различных признаков даст минимум среднего числа шагов. Для
рассмотренная процедура при одинаковой информативности различных признаков даст минимум среднего числа шагов. Для  последовательную процедуру ввёл Вальд и назвал её последовательным критерием отношения вероятностей (п.к.о.в.).
последовательную процедуру ввёл Вальд и назвал её последовательным критерием отношения вероятностей (п.к.о.в.).
Для 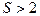 оптимальность процедуры не доказана.
оптимальность процедуры не доказана.
При известных априорных вероятностях можно реализовать байесовскую последовательную процедуру, а если известны затраты на измерения признаков и матрица штрафов за неверное распознавание, то последовательную процедуру можно остановить по минимуму среднего риска. Суть здесь заключена в сравнении потерь, вызванных ошибками распознавания при прекращении процедуры, и ожидаемых потерь после следующего измерения плюс затраты на это измерение. Такая задача решается методом динамического программирования, если последовательные измерения статистически независимы. Более подробные сведения об оптимизации байесовской последовательной процедуры можно почерпнуть в рекомендованной литературе [8].
1.17 Аппроксимационный метод оценки распределений
по выборке
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Этот подход мы рассматриваем отдельно потому, что по своим свойствам он достаточно универсален. Кроме оценки (восстановления) распределений, он позволяет попутно решать задачу таксономии, оптимизированного управления последовательной процедурой измерения признаков, даже если они статистически зависимы, облегчает оценку информативности признаков и решение некоторых задач анализа экспериментальных данных.
В основе метода лежит предположение о том, что неизвестное (восстанавливаемое) распределение значений признаков каждого образа хорошо аппроксимируется смесью базовых распределений достаточно простого и заранее известного вида

где 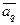 – множество (вектор) параметров
– множество (вектор) параметров 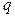 -го базового распределения,
-го базового распределения, 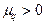 – весовые коэффициенты, удовлетворяющие условию
– весовые коэффициенты, удовлетворяющие условию  . Чтобы не загромождать формулу, в ней опущен индекс номера образа, который описывается данным распределением значений признаков.
. Чтобы не загромождать формулу, в ней опущен индекс номера образа, который описывается данным распределением значений признаков.
Представление неизвестного распределения в виде ряда используется, например, в методе потенциальных функций. Однако там 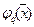 являются элементами полной ортогональной системы функций. С одной стороны, это хорошо, потому что вычисление
являются элементами полной ортогональной системы функций. С одной стороны, это хорошо, потому что вычисление  первых значений
первых значений  гарантирует минимум среднеквадратического отклонения восстановленного распределения от истинного. Но с другой стороны,
гарантирует минимум среднеквадратического отклонения восстановленного распределения от истинного. Но с другой стороны, 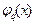 не являются распределениями, могут быть знакопеременными, что при
не являются распределениями, могут быть знакопеременными, что при 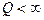 , как правило, приводит к неприемлемому эффекту, когда для некоторых значений
, как правило, приводит к неприемлемому эффекту, когда для некоторых значений  восстановленное распределение
восстановленное распределение 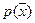 является отрицательным. Попытки избежать этого эффекта далеко не всегда являются успешными. Этого недостатка лишён рассматриваемый подход, когда искомое распределение представлено смесью базовых. При этом
является отрицательным. Попытки избежать этого эффекта далеко не всегда являются успешными. Этого недостатка лишён рассматриваемый подход, когда искомое распределение представлено смесью базовых. При этом  называют распределениями компонент смеси, а
называют распределениями компонент смеси, а  и
и  – её параметрами. У этого подхода при очевидных достоинствах имеются недостатки. В частности, решение задачи оценки параметров смеси является, вообще говоря, многоэкстремальным, и нет гарантий, что найденное решение находится в глобальном экстремуме, если исключить неприемлемый на практике полный перебор вариантов разбиения смеси на компоненты.
– её параметрами. У этого подхода при очевидных достоинствах имеются недостатки. В частности, решение задачи оценки параметров смеси является, вообще говоря, многоэкстремальным, и нет гарантий, что найденное решение находится в глобальном экстремуме, если исключить неприемлемый на практике полный перебор вариантов разбиения смеси на компоненты.
Такие понятия, как “смесь”, “компонента” обычно используются при решении задач таксономии, но это не является помехой для описания в виде смеси достаточно общего вида распределения значений признаков того или иного образа. Аппроксимационный метод является как бы промежуточным между параметрическим и непараметрическим оцениванием распределений. Действительно, по выборке приходится оценивать значения параметров  и
и  , и в то же время вид закона распределения заранее неизвестен, на него наложены лишь самые общие ограничения. Например, если компонента – нормальный закон, то плотность вероятности
, и в то же время вид закона распределения заранее неизвестен, на него наложены лишь самые общие ограничения. Например, если компонента – нормальный закон, то плотность вероятности 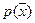 не должна обращаться в нуль при всех
не должна обращаться в нуль при всех  и быть достаточно гладкой. Если компонента – биномиальный закон, то
и быть достаточно гладкой. Если компонента – биномиальный закон, то 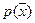 может быть практически любым дискретным распределением.
может быть практически любым дискретным распределением.
Вместе с тем параметры смеси определить классическими методами параметрического оценивания (например, методом моментов или максимума функции правдоподобия) не представляется возможным за редкими исключениями (частными случаями). В связи с этим целесообразно обратиться к методам, используемым при решении задач таксономии. 
В качестве компонент удобно использовать биномиальные законы для дискретных признаков и нормальные плотности вероятностей для непрерывных признаков, так как свойства и теория этих распределений хорошо изучены. К тому же они, как показывают практические приложения, в качестве компонент достаточно адекватно описывают весьма широкий класс распределений.
Нормальный закон, как известно, характеризуется вектором средних значений признаков и матрицей ковариаций. Особое место в ряде задач занимают нормальные законы с диагональными ковариационными матрицами (в компонентах признаки статистически независимы). При этом удаётся оптимизировать последовательную процедуру измерения признаков, даже если в восстановленном распределении 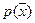 признаки зависимы. Рассмотрение этого вопроса выходит за рамки курса. Интересующиеся могут обратиться к рекомендованной литературе [2].
признаки зависимы. Рассмотрение этого вопроса выходит за рамки курса. Интересующиеся могут обратиться к рекомендованной литературе [2].
Для облегчения понимания аппроксимационного метода будем рассматривать упрощённый вариант, а именно: одномерные распределения.
Итак,

где 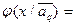 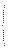
| 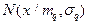 – для непрерывных признаков, – для непрерывных признаков, 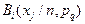 – для дискретных признаков, – для дискретных признаков,
|
 – вектор параметров базового распределения (компоненты),
– вектор параметров базового распределения (компоненты),
 – весовой коэффициент
– весовой коэффициент  -й компоненты,
-й компоненты,
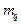 – математическое ожидание
– математическое ожидание  -й нормальной компоненты,
-й нормальной компоненты,
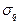 – среднеквадратическое отклонение
– среднеквадратическое отклонение  -й нормальной компоненты,
-й нормальной компоненты,
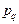 – параметр
– параметр  -й биномиальной компоненты,
-й биномиальной компоненты,
 – число градаций дискретного признака,
– число градаций дискретного признака,


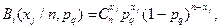
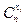 – число сочетаний из
– число сочетаний из 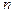 по
по  .
.
При достаточно большом 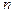 вместо биномиального закона можно использовать нормальный.
вместо биномиального закона можно использовать нормальный.
Теперь предстоит оценить значения параметров. Если рассматривать смесь нормальных законов, то следует отметить, что метод максимума правдоподобия неприменим, когда все параметры смеси неизвестны. В таком случае можно воспользоваться разумно организованными итерационными процедурами. Рассмотрим одну из них.
Для начала зафиксируем  , то есть будем считать его заданным. Каждому объекту
, то есть будем считать его заданным. Каждому объекту  выборки поставим в соответствие апостериорную вероятность
выборки поставим в соответствие апостериорную вероятность  принадлежности его
принадлежности его  -й компоненте смеси:
-й компоненте смеси:

Легко видеть, что для всех 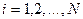 выполняются условия
выполняются условия 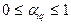 и
и  . Если известны
. Если известны  для всех
для всех 
 , то можно определить
, то можно определить  методом максимума правдоподобия
методом максимума правдоподобия 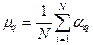 .
.
Функцию правдоподобия  -й компоненты смеси определим следующим образом
-й компоненты смеси определим следующим образом 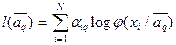 , и оценки максимального правдоподобия
, и оценки максимального правдоподобия 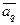 можно получить из уравнения
можно получить из уравнения 
Таким образом, зная 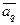 и
и  , можно определить
, можно определить  , и наоборот, зная
, и наоборот, зная  , можно определить
, можно определить 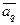 и
и  , то есть параметры смеси. Но ни то, ни другое неизвестно. В связи с этим воспользуемся следующей процедурой последовательных приближений:
, то есть параметры смеси. Но ни то, ни другое неизвестно. В связи с этим воспользуемся следующей процедурой последовательных приближений:
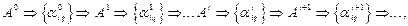
где 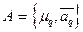 ,
, 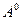 – произвольно заданные начальные значения параметров смеси, верхний индекс – номер итерации в последовательной процедуре вычислений.
– произвольно заданные начальные значения параметров смеси, верхний индекс – номер итерации в последовательной процедуре вычислений.
Известно, что эта процедура является сходящейся и при 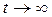 пределом служат оценки неизвестных параметров
пределом служат оценки неизвестных параметров  смеси, дающие максимум функции правдоподобия
смеси, дающие максимум функции правдоподобия
 ,
,
причём 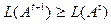 и
и  стремится к нулю при
стремится к нулю при  .
.
Для одномерного нормального закона
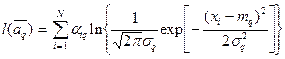 .
.
Решая уравнение 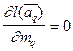 и
и 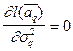 , получим для
, получим для  -го шага
-го шага  ,
, 
После завершения последовательной процедуры вычисляются  . Соответствующие вычислительные формулы для многомерных нормальных распределений можно найти в работе [2].
. Соответствующие вычислительные формулы для многомерных нормальных распределений можно найти в работе [2].
Получаемые в результате рассмотренной последовательной процедуры значения параметров являются оценками максимального правдоподобия как относительно каждой компоненты, так и относительно смеси в целом.
Если 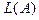 имеет несколько максимумов, то итерационный процесс в зависимости от заданных начальных значений
имеет несколько максимумов, то итерационный процесс в зависимости от заданных начальных значений 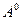 сходится к одному из них, не обязательно глобальному. Преодолеть этот недостаток, присущий практически всем методам оценок параметров многомерных распределений (по крайней мере, смесей) достаточно сложно. В частности, можно повторить последовательную процедуру несколько раз при различных
сходится к одному из них, не обязательно глобальному. Преодолеть этот недостаток, присущий практически всем методам оценок параметров многомерных распределений (по крайней мере, смесей) достаточно сложно. В частности, можно повторить последовательную процедуру несколько раз при различных 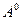 и выбрать наилучшее из решений. Выбор различных
и выбрать наилучшее из решений. Выбор различных 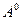 осуществляют либо случайным образом, либо с помощью различного рода направленных процедур. Скорость сходимости
осуществляют либо случайным образом, либо с помощью различного рода направленных процедур. Скорость сходимости 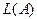 к максимуму тем выше, чем сильнее разнесены компоненты в признаковом пространстве и чем ближе выбранные
к максимуму тем выше, чем сильнее разнесены компоненты в признаковом пространстве и чем ближе выбранные 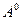 к значениям
к значениям  , соответствующим максимуму функции правдоподобия.
, соответствующим максимуму функции правдоподобия.
Мы рассмотрели метод оценки параметров смеси при фиксированном числе компонент  . Но в аппроксимационном методе и
. Но в аппроксимационном методе и  следует определить, оптимизируя какой-либо критерий. Предлагается следующий подход. Оцениваются последовательно параметры
следует определить, оптимизируя какой-либо критерий. Предлагается следующий подход. Оцениваются последовательно параметры 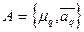 при
при  . Из полученного ряда
. Из полученного ряда  выбирается в некотором смысле лучшее значение
выбирается в некотором смысле лучшее значение 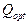 .
.
Воспользуемся мерой неопределённости К. Шеннона  для поиска
для поиска 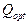 :
:
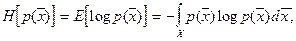
где  – энтропия распределения
– энтропия распределения 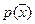 ,
,
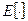 – знак математического ожидания,
– знак математического ожидания,
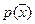 – плотность вероятности значений непрерывных признаков.
– плотность вероятности значений непрерывных признаков.
При последовательном увеличении значений  имеют место две тенденции:
имеют место две тенденции:
· уменьшение энтропии за счёт разделения выборки на части с уменьшающимся разбросом значений наблюдаемых величин 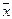 внутри подвыборок (компонент смеси);
внутри подвыборок (компонент смеси);
· увеличение энтропии за счёт уменьшения объёма подвыборок и связанным с этим увеличением статистик, характеризующих разброс значений 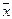 .
.
Наличие этих двух тенденций обуславливает существование 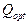 по критерию наименьшего значения дифференциальной энтропии (рис. 23). Чтобы использовать на практике этот критерий, необходимо в явном виде выразить оценку компонент смеси через объём подвыборки, формирующей эту компоненту. Такие соотношения получены для нормальных и биномиальных распределений. Для простоты рассмотрим одномерное нормальное распределение. Воспользуемся его байесовской оценкой
по критерию наименьшего значения дифференциальной энтропии (рис. 23). Чтобы использовать на практике этот критерий, необходимо в явном виде выразить оценку компонент смеси через объём подвыборки, формирующей эту компоненту. Такие соотношения получены для нормальных и биномиальных распределений. Для простоты рассмотрим одномерное нормальное распределение. Воспользуемся его байесовской оценкой
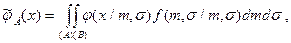
где  – область определения
– область определения  ,
,
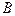 – область определения
– область определения  ,
,
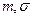 – выборочные оценки
– выборочные оценки  и
и  .
.
В соответствии с формулой Байеса


Рис. 23. Иллюстрация тенденций, формирующих 
Если априорное распределение  неизвестно, то целесообразно использовать равномерное распределение по всей области
неизвестно, то целесообразно использовать равномерное распределение по всей области 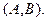
Опустив все выкладки, которые приведены в работе [2], сообщим лишь, что получается распределение, не являющееся гауссовым, но асимптотически сходящееся к нему (при 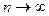 ). Среднее значение
). Среднее значение 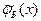 равно среднему значению, определённому по выборке, а дисперсия равна выборочной дисперсии
равно среднему значению, определённому по выборке, а дисперсия равна выборочной дисперсии  , умноженной на коэффициент
, умноженной на коэффициент 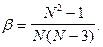
Можно показать, что  хорошо аппроксимируется нормальным законом с математическим ожиданием, равным
хорошо аппроксимируется нормальным законом с математическим ожиданием, равным  – выборочному среднему, и дисперсией, равной выборочной дисперсии
– выборочному среднему, и дисперсией, равной выборочной дисперсии  , умноженной на
, умноженной на  . Как видно из формулы,
. Как видно из формулы,  стремится к единице при
стремится к единице при 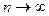 , возрастает с уменьшением
, возрастает с уменьшением  и накладывает ограничения на объём выборки
и накладывает ограничения на объём выборки 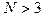 (рис. 24).
(рис. 24).

Рис. 24. Зависимость поправочного коэффициента b
от объёма выборки N
Таким образом, нам удалось в явной форме выразить зависимость параметров компонент смеси от объёма подвыборок, что, в свою очередь, позволяет реализовать процедуру поиска 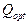 .
.
Объём подвыборки для q -й компоненты смеси определяется по формуле  .
.
Итак, рассмотрен вариант оценки параметров смеси. Он не является статистически строго обоснованным, но все вычислительные процедуры опираются на критерии, принятые в математической статистике. Многочисленные практические приложения аппроксимационного метода в различных предметных областях показали его эффективность и не противоречат ни одному из допущений, изложенных в данном разделе.
Более подробное и углублённое изложение аппроксимационного метода желающие могут найти в рекомендованной литературе [2], [4].
|
|
