Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Параметрическое оценивание распределений

Параметрическое оценивание распределений реализуется в тех случаях, когда известен вид распределений и по обучающей выборке необходимо лишь оценить значения параметров этих распределений. Априорное знание вида на практике встречается нечасто, однако, учитывая удобство данного подхода, иной раз делают допущение, например, о том, что - нормальный закон. Такого рода допущения далеко не всегда имеют убедительные основания, но тем не менее используются, если результаты обучения приводят к приемлемым ошибкам распознавания.

Итак, обучение сводится к оценке значений параметров при заранее известном виде этих распределений. Особое место среди распределений занимает нормальный закон. Это связано с тем, что, как известно из математической статистики, если случайная величина порождена воздействием достаточно большого числа случайных факторов с произвольными законами распределения и среди этих влияний нет явно доминирующего, то интересующая нас величина имеет нормальный закон распределения. Для одномерного случая

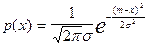
(для простоты впредь будем рассматривать одномерный случай, а заинтересовавшиеся слушатели могут обратиться к литературе, приведённой в конце конспекта лекций).

Параметрами этого распределения являются две величины: – математическое ожидание, – дисперсия. Их-то и нужно оценить по выборке. Одним из наиболее простых является метод моментов. Он применим для распределений 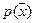, зависящих от параметров, имеющих конечных первых моментов, которые могут быть выражены как явные функции 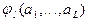параметров 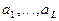. Тогда, вычислив по выборке первых её моментов и приравняв их , получим систему уравнений

,

из которой определяются оценки .

Для одномерного нормального закона

.

.