Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Таксономия

Статистических методов решения задач таксономии существует достаточно много. Мы из-за ограниченности времени, выделенного на курс распознавания образов (классификации), остановимся только на одном, не умаляя значения или эффективности других методов.

Он непосредственно связан с аппроксимационным методом распознавания. Действительно, восстановление неизвестного распределения по выборке в виде смеси базовых распределений является, по существу, решением задачи таксономии с определёнными требованиями (ограничениями), предъявляемыми к описанию каждого из таксонов.

Рис. 25. Объединение компонент смеси в таксоны

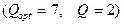
Эти требования состоят в том, что значения признаков объектов, входящих в один таксон, имеют распределения вероятностей заданного вида. В рассматриваемом нами случае это нормальные или биномиальные распределения. В ряде случаев это ограничение можно обойти. В частности, если задано число таксонов , а , то некоторые таксоны следует объединить в один, который будет иметь уже отличающееся от нормального или биномиального распределение значений признаков (рис. 25).

Естественно, объединять в один таксон следует те компоненты смеси, которые наименее разнесены в признаковом пространстве. Мерой разнесённости компонент может служить, например, мера Кульбака

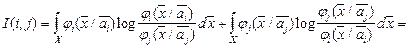
Следует отметить, что эта мера применима лишь в том случае, если подмножество значений , на котором 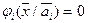, а 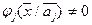и наоборот, пусто. В частности, это требование выполняется для нормально распределённых значений признаков компонент смеси.

Если говорить о связи изложенного статистического подхода к таксономии с ранее рассмотренными детерминистскими методами, то можно заметить следующее.

Алгоритм ФОРЭЛЬ близок по своей сути к аппроксимации распределения смесью нормальных плотностей вероятностей значений признаков, причём матрицы ковариаций компонент смеси диагональны, элементы этих матриц равны между собой, распределения компонент отличаются друг от друга только векторами средних значений. Однако на одинаковый результат таксономии даже в этом случае можно рассчитывать лишь при большой разнесённости компонент смеси. Объединение нескольких смесей в один таксон по методике близко к эмпирическому алгоритму KRAB 2. Эти два подхода взаимно дополняют друг друга. Когда выборка мала и статистические методы неприменимы или малоэффективны, целесообразно использовать алгоритм KRAB, FOREL, KRAB 2. При большом объёме выборки эффективнее становятся статистические методы, в том числе объединение компонент смеси в таксоны.