Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Правило ближайшего соседа

Пусть – множество объектов обучающей последовательности, то есть принадлежность каждого из них тому или иному образу достоверно известна. Пусть также 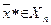является объектом, ближайшим к распознаваемому . Напомним, что при этом правило ближайшего соседа для классификации 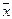состоит в том, что 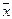относят к тому классу (образу), которому принадлежит 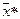. Естественно, такое отнесение носит случайный характер. Вероятность того, что 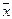будет отнесён к 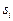, есть апостериорная вероятность . Если 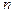очень велико, то вполне можно допустить, что 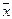расположен достаточно близко к 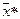, настолько близко, что . А это есть не что иное, как рандомизированное решающее правило: 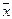относят к 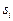с вероятностью 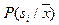. Байесовское решающее правило основано на выборе максимальной апостериорной вероятности, то есть 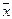относят к в том случае, если

.

Отсюда видно, что если близка к единице, то правило ближайшего соседа даёт решение, в большинстве случаев совпадающее с байесовским. Напомним, что эти рассуждения имеют достаточные основания лишь при очень больших 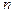(объёмах обучающей выборки). Такие условия на практике встречаются не часто, но позволяют понять статистический смысл правила ближайшего соседа.