
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод максимума правдоподобия
|
|
Функция правдоподобия, введённая Фишером, выглядит следующим образом:
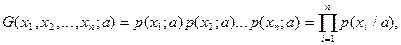
где 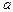 – неизвестный параметр.
– неизвестный параметр.
В качестве оценки параметра 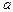 нужно выбрать такую величину, при которой
нужно выбрать такую величину, при которой 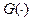 достигает максимума. Поскольку
достигает максимума. Поскольку 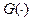 достигает максимума при том же
достигает максимума при том же 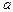 , что и
, что и  , то поиск требуемого значения оценки
, то поиск требуемого значения оценки 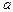 состоит в решении уравнения правдоподобия
состоит в решении уравнения правдоподобия  . При этом все корни
. При этом все корни  следует отбросить, а оставить только те, которые зависят от
следует отбросить, а оставить только те, которые зависят от  .
.
Оценка параметра распределения является случайной величиной, которая имеет математическое ожидание и " рассеяние" вокруг него. Оценка называется эффективной, если её " рассеяние" вокруг своего математического ожидания минимально.
Справедлива следующая теорема (приводится без доказательства). Если существует для 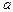 эффективная оценка
эффективная оценка  , то уравнение правдоподобия имеет единственное решение. Это решение при
, то уравнение правдоподобия имеет единственное решение. Это решение при 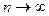 сходится к истинному значению
сходится к истинному значению 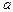 .
.
Всё это справедливо и при нескольких неизвестных параметрах. Например, для одномерного нормального закона
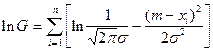 ,
,
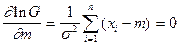 ,
,
отсюда  при
при 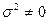 .
.
 ,
,
отсюда 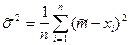 .
.
Оценка называется несмещённой, если математическое ожидание  оценки
оценки  равно
равно 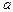 . Оценка
. Оценка  является несмещённой. Действительно, поскольку
является несмещённой. Действительно, поскольку 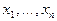 – простой случайный выбор из генеральной совокупности, то
– простой случайный выбор из генеральной совокупности, то  и
и  .
.
Выясним, является ли 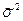 , полученная методом максимума правдоподобия (или методом моментов), несмещённой. Легко убедиться, что
, полученная методом максимума правдоподобия (или методом моментов), несмещённой. Легко убедиться, что
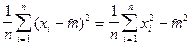 .
.
Следовательно,

 .
.
Найдём математическое ожидание этой величины:
 .
.
Так как дисперсия 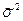 не зависит от значения
не зависит от значения  , то выберем
, то выберем  . Тогда
. Тогда
 ,
,  ,
, 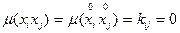 ,
,
где  ,
,  – коэффициент корреляции между
– коэффициент корреляции между 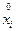 и
и  (в данном случае он равен нулю, т.к.
(в данном случае он равен нулю, т.к.  и
и 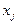 не зависят друг от друга).
не зависят друг от друга).
Итак,  . Отсюда видно, что оценка
. Отсюда видно, что оценка 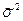 не является несмещённой, её математическое ожидание несколько меньше, чем
не является несмещённой, её математическое ожидание несколько меньше, чем  . Для ликвидации данного смещения необходимо умножить
. Для ликвидации данного смещения необходимо умножить 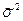 на
на  . В результате получим несмещённую оценку
. В результате получим несмещённую оценку
 .
.
1.14 Случай статистически независимых признаков
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
При статистически независимых признаках существенно упрощается решение задач распознавания. В частности, при оценивании распределений  вместо многомерных плотностей вероятности достаточно оценить
вместо многомерных плотностей вероятности достаточно оценить  одномерных плотностей
одномерных плотностей 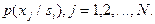
В связи с этим рассмотренные нами примеры одномерных распределений не только носят иллюстративный характер, но могут непосредственно использоваться при решении практических задач, если есть убедительные основания считать признаки, характеризующие объекты распознавания, статистически независимыми. При этом

и формула Байеса, используемая для вычисления апостериорной вероятности принадлежности объекта с признаками 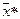 образу
образу 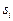 , принимает вид
, принимает вид

Встречаются практические приложения теории распознавания, когда признаки считают статистически независимыми без веских на то оснований, а то и зная, что на самом деле признаки (хотя бы часть из них) взаимозависимы. Это делается для упрощения процедур обучения и распознавания в ущерб " качеству" (вероятности ошибок), если этот ущерб можно признать приемлемым.
Особенно заметно упрощение процедуры распознавания по методу Байеса, если признаки принимают двоичные значения. В этом случае обучение состоит в построении следующей таблицы:
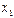
| 
|  
| ... | 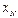
| ||
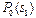
| 
| 
| 
| 
| ... | 
|

| 
| 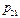
| 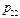
| 
| ... | 
|

| 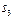
| 
| 
| 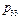
| ... | 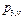
|
| . . . | . . . | . . . | . . . | . . . | . . . | . . . |

| 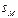
| 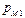
| 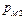
| 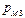
| ... | 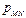
|
Здесь  ,
, 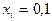 .
.
Если  не очень велико, то отнесение неизвестного объекта к тому или иному образу настолько упрощается, что зачастую нет необходимости использовать компьютер, достаточно калькулятора, а в крайнем случае можно осуществить расчёт вручную. Только необходимо иметь заранее подготовленную таблицу со значениями
не очень велико, то отнесение неизвестного объекта к тому или иному образу настолько упрощается, что зачастую нет необходимости использовать компьютер, достаточно калькулятора, а в крайнем случае можно осуществить расчёт вручную. Только необходимо иметь заранее подготовленную таблицу со значениями 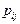 (точнее, с их оценками). Если у неизвестного объекта выявлено наличие тех или иных признаков, то для каждого из образов в соответствующей строке таблицы выбираются те
(точнее, с их оценками). Если у неизвестного объекта выявлено наличие тех или иных признаков, то для каждого из образов в соответствующей строке таблицы выбираются те 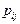 , которые связаны с этими признаками, и перемножаются. Объект относят к тому классу, произведение для которого получилось максимальным. При этом, конечно, осуществляется домножение на априорные вероятности, а нормировку апостериорных вероятностей можно не осуществлять, т.к. она не влияет на результат выбора максимума по
, которые связаны с этими признаками, и перемножаются. Объект относят к тому классу, произведение для которого получилось максимальным. При этом, конечно, осуществляется домножение на априорные вероятности, а нормировку апостериорных вероятностей можно не осуществлять, т.к. она не влияет на результат выбора максимума по  .
.
Если признаки дискретны, но многозначны, то к двоичным значениям нетрудно перейти путём специальной двоичной кодировки.
1.15 Распознавание при неизвестных априорных вероятностях
образов
 могут быть неизвестны по многим причинам, в частности, если они являются неизвестными функциями времени или каких-либо неконтролируемых обстоятельств, условий. В этом случае использовать байесовское решающее правило невозможно. Вместо риска потерь (в частном случае средней вероятности ошибок распознавания) приходится иметь дело с вектором (в частном случае
могут быть неизвестны по многим причинам, в частности, если они являются неизвестными функциями времени или каких-либо неконтролируемых обстоятельств, условий. В этом случае использовать байесовское решающее правило невозможно. Вместо риска потерь (в частном случае средней вероятности ошибок распознавания) приходится иметь дело с вектором (в частном случае 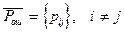 ).
).
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
|
|
