Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

править] Критерий отрицательной определённости квадратичной формы

Доказательство сводится к предыдущему случаю, так как матрица A является отрицательно определённой тогда и только тогда, когда матрица − A является положительно определённой. При замене матрицы A на противоположную главные миноры нечётного порядка меняют знак, а главные миноры чётного порядка остаются такими же.

Условие сходимости итерационного процесса ~ Метод Якоби ~ Метод Зейделя ~ Метод простой итерации

Рассматривается система Ax = b.
Для применения итерационных методов система должна быть приведена к эквивалентному виду x=Bx+d. Затем выбирается начальное приближение к решению системы уравнений
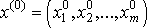и находится последовательность приближений к корню. Для сходимости итерационного процесса достаточно, чтобы было выполнено условие 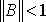. Критерий окончания итераций зависит от применяемого итерационного метода.

Метод Якоби.

Самый простой способ приведения системы к виду удобному для итерации состоит в следующем: из первого уравнения системы выразим неизвестное x ₁, из второго уравнения системы выразим x ₂, и т. д. В результате получим систему уравнений с матрицей B, в которой на главной диагонали стоят нулевые элементы, а остальные элементы вычисляются по формулам:

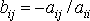, i, j = 1, 2,... n.

Компоненты вектора d вычисляются по формулам:

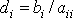, i = 1, 2,... n.

Расчетная формула метода простой итерации имеет вид

,

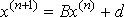или в покоординатной форме записи выглядит так:

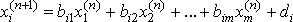, i = 1, 2,... m.

Критерий окончания итераций в методе Якоби имеет вид:

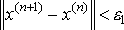, где .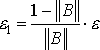

Если 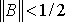, то можно применять более простой критерий

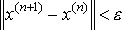окончания итераций

ПРИМЕР 1. Решение системы линейных уравнений методом Якоби.

Метод Зейделя.

Метод можно рассматривать как модификацию метода Якоби. Основная идея состоит в том, что при вычислении очередного (n+1)-го приближения к неизвестному x _i при i > 1 используют уже найденные (n+1)-е приближения к неизвестным x ₁, x ₂,..., x _{i - 1}, а не n-ое приближение, как в методе Якоби. Расчетная формула метода в покоординатной форме записи выглядит так:

,

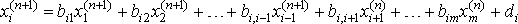i = 1, 2,... m.. Условия сходимости и критерий окончания итераций можно взять такими же как в методе Якоби.

ПРИМЕР 2. Решение систем линейных уравнений методом Зейделя.

Пусть матрица системы уравнений A - симметричная и положительно определенная. Тогда при любом выборе начального приближения метод Зейделя сходится. Дополнительных условий на малость нормы некоторой матрицы здесь не накладывается.

Метод простой итерации.

Если A - симметричная и положительно определенная матрица, то систему уравнений часто приводят к эквивалентному виду:

x = x - (A x - b), - итерационный параметр.

Расчетная формула метода простой итерации в этом случае имеет вид:

x ⁽ⁿ⁺¹⁾ = x ⁿ - (A x ⁿ - b).

Здесь B = E - A и параметр > 0 выбирают так, чтобы по возможности сделать минимальной величину .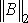

Пусть 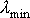и 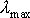- минимальное и максимальное собственные значения матрицы A. Оптимальным является выбор параметра 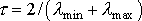. В этом случае 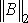принимает минимальное значение равное .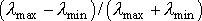