Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Приведение квадратичных форм к каноническому виду

Рассмотрим некоторое линейное преобразование А с матрицей.

Это симметрическое преобразование можно записать в виде:

y₁ = a₁₁x₁ + a₁₂x₂

y₂ = a₁₂x₁ + a₂₂x₂

где у₁ и у₂ – координаты вектора в базисе.

Очевидно, что квадратичная форма может быть записана в виде

Ф(х₁, х₂) = х₁у₁ + х₂у₂.

Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х₁ и х₂ – скалярное произведение.

Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.

Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:

.

При переходе к новому базису от переменных х₁ и х₂ мы переходим к переменным и. Тогда:

Тогда.

Выражение называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.

Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.

Пример. Привести к каноническому виду квадратичную форму

Ф(х₁, х₂) = 27.

Коэффициенты: а₁₁ = 27, а₁₂ = 5, а₂₂ = 3.

Составим характеристическое уравнение:;

(27 - l)(3 - l) – 25 = 0

l² - 30l + 56 = 0

l₁ = 2; l₂ = 28;

Пример. Привести к каноническому виду уравнение второго порядка:

17x² + 12xy + 8y² – 20 = 0.

Коэффициенты а₁₁ = 17, а₁₂ = 6, а₂₂ = 8. А =

Составим характеристическое уравнение:

(17 - l)(8 - l) - 36 = 0

136 - 8l - 17l + l² – 36 = 0

l² - 25l + 100 = 0

l₁ = 5, l₂ = 20.

Итого: - каноническое уравнение эллипса.

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение: Составим характеристическое уравнение квадратичной формы: при

Решив это уравнение, получим l₁ = 2, l₂ = 6.

Найдем координаты собственных векторов:

полагая m₁ = 1, получим n₁ =

полагая m₂ = 1, получим n₂ =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение: Составим характеристическое уравнение квадратичной формы: при

Решив это уравнение, получим l₁ = 1, l₂ = 11.

Найдем координаты собственных векторов:

полагая m₁ = 1, получим n₁ =

полагая m₂ = 1, получим n₂ =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

4ху + 3у² + 16 = 0

Коэффициенты: a₁₁ = 0; a₁₂ = 2; a₂₂ = 3.

Характеристическое уравнение:

Корни: l₁ = -1, l₂ = 4.

Для l₁ = -1 Для l₂ = 4

m₁ = 1; n₁ = -0, 5; m₂ = 1; n₂ = 2;

= (1; -0, 5) = (1; 2)

Получаем: -каноническое уравнение гиперболы.

Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.

Пусть квадратичная форма имеет в каком-то базисе матрицу

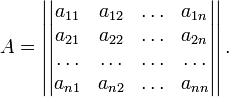
Тогда эта форма положительно определена, если и только если все её главные (угловые) миноры Δ _i положительны. Форма отрицательно определена, если и только если знаки Δ _i чередуются, причём Δ ₁ < 0. Здесь главными минорами матрицы A называются определители вида

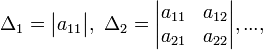
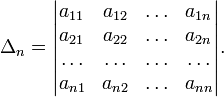
Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица

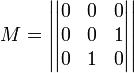
не является неотрицательно определённой — так как, например, (Mv, v) = − 2 для v = (0, 1, − 1). В то же время все её главные миноры равны 0, то есть неотрицательны.