Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Определение. означает одно из множеств: рациональных, или вещественных, или комплексных чисел.

Квадратичная форма

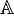означает одно из множеств: 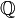рациональных, или 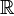вещественных, или 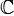комплексных чисел.

Определение

Квадратичной формой над множеством 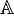называют однородный полином второй степени с коэффициентами из 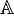; если переменные обозначить 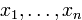, то общий вид квадратичной формы от этих переменных:

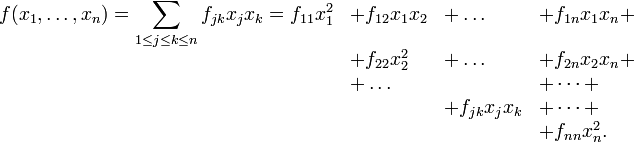
П

Функции

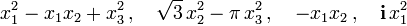
являются квадратичными формами. Функции

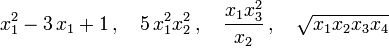
не являются квадратичными формами.

Заметим, что в выражении для квадратичной формы присутствуют как квадраты переменных 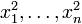так и их смешанные произведения 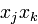. Говорят, что квадратичная форма 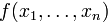имеет канонический вид если в ее представлении все коэффициенты при смешанных произведениях переменных равны нулю, т.е. она имеет вид

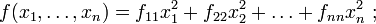
говорят также, что форма является «суммой квадратов»1).

Оказывается, что в любой квадратичной форме можно так сгруппировать входящие в нее одночлены, что в результате получится ее (эквивалентное) представление в виде суммы квадратов.

П