Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Свойства определителей второго и третьего порядков

Будем рассматривать в дальнейшем только определители 3-го порядка. Для определителей 2-го порядка все свойства аналогичны.

1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (операция транспонирования), т.е.

.

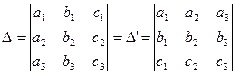Действительно,

Δ =а₁b₂с₃+b₁с₂а₃+с₁а₂b₃—с₁b₂а₃—а₁с₂b₃—b₁a₂c₃. (*)

Δ '=а₁b₂с₃+c₁a₂b₃+b₁с₂а₃+с₁b₂а₃+а₁с₂b₃+b₁а₂с₃. (**)

Сравнивая равенства (*) и (**), получаем, что Δ =Δ '.

2. При перестановке 2-х строк (столбцов) местами определитель меняет знак на противоположный.

Доказательство проводится проверкой.

3. Если определитель имеет 2 одинаковые строки (столбца), то он равен нулю.

Действительно, при перестановке двух одинаковых строк, определитель Δ, очевидно не изменится. С другой стороны, по свойству 2 он изменит знак на противоположный. Следовательно, Δ = -Δ, т.е. Δ =О.

4. При умножении любой строки (столбца) определителя Δ на некоторое число λ, определитель умножается на это число, то есть, например,

.

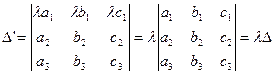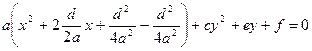
Применим формулы параллельного переноса

, ,

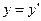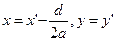
Тогда уравнение примет вид

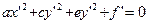
где 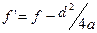. Если же с ≠ 0 и е ≠ 0, то аналогичным образом исключаем в полученном уравнении член с у.

Итак можно считать, что КВП представляется одним из трёх видов уравнений:

ах ² + by ² + c = 0;

ах ² + by + c = 0;

аy ² + bх + c = 0.

Рассмотрим случаи:

1) с ≠ 0. Тогда

Если – (а/с) › 0 и – (b/c) › 0, то это уравнение эллипса.

Если – (a/c) ‹ 0 b – (b/c) ‹ 0, то получаем пустое множество точек на плоскости.

Если – (a/c) › 0 и – (b/c) ‹ 0, то уравнение гиперболы.

Аналогичным образом получам гиперболу вытянутую вдоль оси ОУ.

2) с = 0. Тогда ах ² + by ² = 0;

Если a и b – разных знаков, то всегда можно считать, что а › 0

b ‹ 0.

Уравнение будет задавать две пересекающиеся прямые ax – by = 0

Если же a и b одного знака, то уравнению удовлетворяет единственная точка О (0, 0).

Вывод: любая кривая второго порядка является эллипсом, гиперболой, параболой, парой пересекающихся прямых, парой параллельных прямых, прямой, точкой или пустым множеством.

Укажем еще один способ классификации КВП.

Тогда
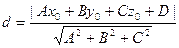