Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Директрисы эллипса и гиперболы.
|
|
Определение. Прямые х=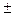 
(а /ε), где ε — эксцентриситет эллипса (гиперболы) называются директрисами эллипса (гиперболы).
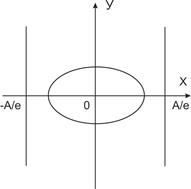
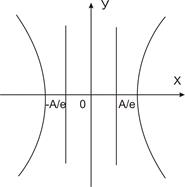
Теорема. Отношение расстояния от любой точки эллипса (гиперболы) до фокуса к расстоянию до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса (гиперболы).
Доказательство, например для эллипса, следует из того, что
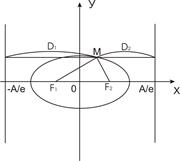MF1=а+ε х, МF2=а—ε х.
Заметим, что, так как все точки параболы равноудалены от директрисы и фокуса, то отношение этих расстояний равно 1. Пo этому можно говорить об эксцентриситете параболы и считать его равным 1. Как
Отметим, что условия параллельности и перпендикулярности прямых l 1 и l 2 равносильны условиям коллинеарности и ортогональности их направляющих векторов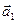 
и 
.
Следовательно,
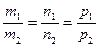
- необходимое и достаточное условие параллельности двух прямых.
m 1 m 2 + n 1 n 2 + p 1 p 2 = 0
- необходимое и достаточное условие перпендикулярности двух прямых.
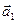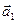Если прямые l 1 и l 2 пересекаются, то величина угла φ между ними равно либо ( ^, ) либо (- ^, ). Следовательно,
|
|
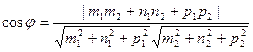