
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическое занятие № 8
|
|
Задача 1 Найти собственные значения и собственные векторы линейного оператора, заданного матрицей  .
.
Решение.
1. Составим характеристическое уравнение данного оператора
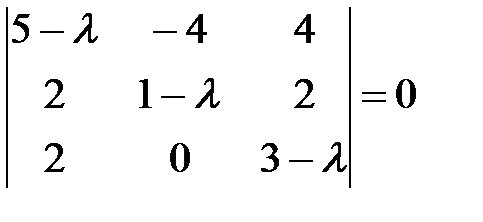 .
.
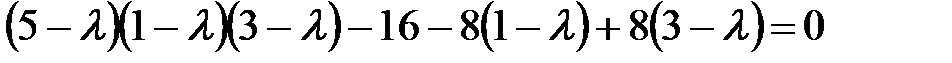 ,
,
 ,
,
 ,
,
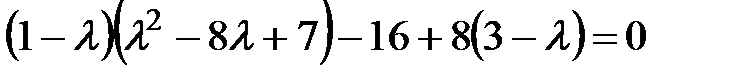 ,
,
 ,
,

 .
.
Найдем корни уравнения.

Получаем: 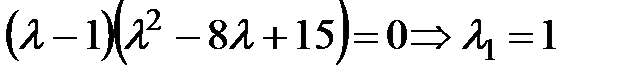 или
или  .
.
Найдем корни второго уравнения.
 ,
,  .
.
 ,
, 
Таким образом, собственные значения равны  ,
,  ,
, 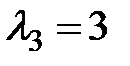 .
.
2. Найдем собственные векторы.
При 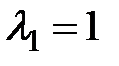 :
:
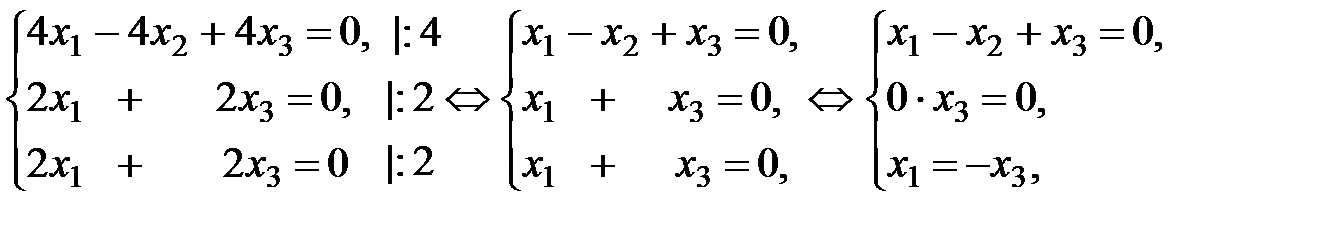

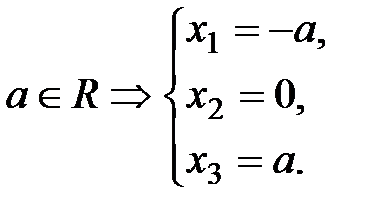
Первый собственный вектор имеет вид  . Пусть
. Пусть  , тогда
, тогда  .
.
При  :
:


 .
.
Второй собственный вектор имеет вид  . Пусть
. Пусть  , тогда
, тогда  .
.
При 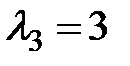 :
:


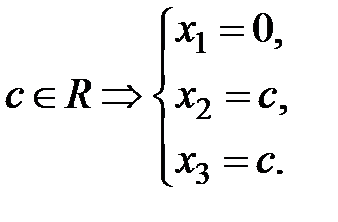
Третий собственный вектор имеет вид  . Пусть
. Пусть 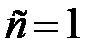 , тогда
, тогда  .
.
Ответ. При 
 ; при
; при 
 ; при
; при 
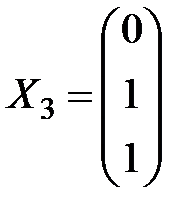
Задача 2 Привести алгебраическое уравнение второй степени к каноническому виду и определить тип кривой, определяемой данным уравнением 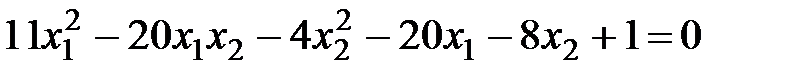 .
.
Решение.
Запишем данное уравнение в матричном виде
 .
.
1) Для того чтобы найти матрицу ортогонального оператора, приводящего квадратичную форму  к каноническому виду, сначала составим характеристическое уравнение
к каноническому виду, сначала составим характеристическое уравнение
det  .
.
Для решения этой части задачи требуется владение методами решений уравнений различных степеней вида 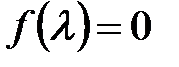 .
.
Решая уравнение, мы получим два действительных корня  .
.
Далее для каждого собственного значения находим собственные векторы, решая однородные системы линейных уравнений.
Для каждой системы будем находить фундаментальную систему решений.
а) 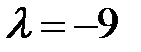





Первый собственный вектор с координатами  . При
. При  первый собственный вектор имеет координаты
первый собственный вектор имеет координаты  . Нормируем данный вектор и получим первый нормированный собственный вектор
. Нормируем данный вектор и получим первый нормированный собственный вектор 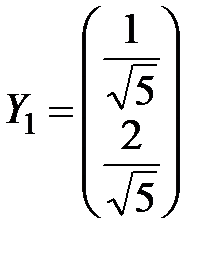 .
.
б) 




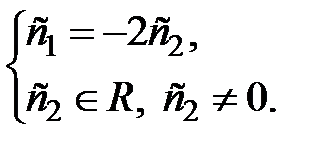
Второй собственный вектор имеет координаты  . Аналогично, получим второй нормированный собственный вектор
. Аналогично, получим второй нормированный собственный вектор  .
.
в) Ортогональный оператор, приводящий квадратичную форму к каноническому виду имеет вид  . Базисные векторы новой системы координат
. Базисные векторы новой системы координат  .
.  ;
;  .
.
Так как det S=1, то  оператор поворота двумерного линейного пространства вокруг начало координат на угол
оператор поворота двумерного линейного пространства вокруг начало координат на угол  такой, что
такой, что  ,
,  . Замечание. Если бы мы получили матрицу такую, что det S=-1, то достаточно было бы поменять местами два собственных вектора.
. Замечание. Если бы мы получили матрицу такую, что det S=-1, то достаточно было бы поменять местами два собственных вектора.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Получим уравнение в новой системе координат 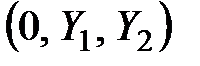 , применяя формулы перехода:
, применяя формулы перехода:  ,
, 
 ,
,
 ,
,
 ,
,
пусть  ,
, 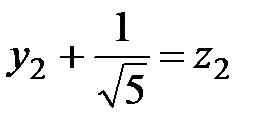 , тогда
, тогда  . Уравнение определяет
. Уравнение определяет
гиперболу, полученную параллельным переносом системы координат  в точку
в точку  . Изобразим кривую
. Изобразим кривую  .
.

Рисунок 125
Задача 3 Выяснить знакоопределенность квадратичной формы  и найти ортогональную матрицу, приводящую квадратичную форму к каноническому виду.
и найти ортогональную матрицу, приводящую квадратичную форму к каноническому виду.
Решение.
Запишем данное уравнение в матричном виде  .
.
Для того чтобы найти матрицу ортогонального преобразования, сначала составим характеристическое уравнение  и найдем собственные значения, используя различные методы решения уравнений третьей степени.
и найдем собственные значения, используя различные методы решения уравнений третьей степени.


 ,
,  .
.
Получены собственные значения:  с кратностью 2 и
с кратностью 2 и  с кратностью 1.
с кратностью 1.
Диагональная матрица имеет вид  или
или 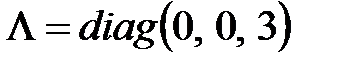 .
.
Далее для каждого собственного значения находим собственные векторы, решая однородные системы линейных уравнений. Для каждой системы будем находить фундаментальную систему решений.
а) 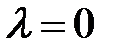 ,
, 
Решаем систему линейных уравнений матричным методом: 


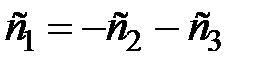 , пусть
, пусть  ,
, 
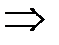
 . Первый собственный вектор:
. Первый собственный вектор:  . Пусть
. Пусть 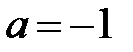 ,
,  , тогда
, тогда  .
.
б) 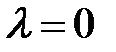
Рассуждая аналогично, получаем второй собственный вектор  со значениями
со значениями  ,
,  ,
,  . Векторы
. Векторы  и
и  не ортогональны.
не ортогональны.
Ортогонализируя  и
и  методом Грамма-Шмидта, получим два ортогональных вектора
методом Грамма-Шмидта, получим два ортогональных вектора 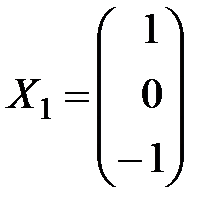 и
и  . Теперь необходимо нормировать эти векторы (разделить каждую координату вектора на ее длину)
. Теперь необходимо нормировать эти векторы (разделить каждую координату вектора на ее длину)  ,
,  .
.
в) Для собственного значения  собственный вектор:
собственный вектор:  .
.
Запишем матрицу ортогонального преобразования  .
.
С помощью матрицы  от старого базиса
от старого базиса  выполняется переход к новому базису
выполняется переход к новому базису  :
:
 ,
,  ,
,  .
.
Задача 4 Привести к каноническому виду уравнение поверхности второго порядка: 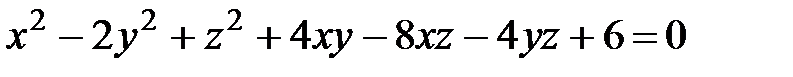 .
.
Решение.
Составим характеристическое уравнение  , или
, или  . Корни этого уравнения:
. Корни этого уравнения:  ,
,  ,
,  .
.
Каноническое уравнение поверхности можем написать сразу:  или
или  .
.
Данная поверхность является однополостным гиперболоидом вращения с полуосями 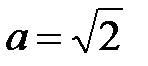 ,
,  ,
,  . Найдем теперь главные направления данной поверхности и формулы преобразования координат, приводящие данное уравнение к каноническому виду. Так как характеристическое уравнение имеет двукратный корень, то нужно действовать согласно указаниям. Составим применительно к нашей задаче систему уравнений:
. Найдем теперь главные направления данной поверхности и формулы преобразования координат, приводящие данное уравнение к каноническому виду. Так как характеристическое уравнение имеет двукратный корень, то нужно действовать согласно указаниям. Составим применительно к нашей задаче систему уравнений: 
Подставим сюда двукратный корень характеристического уравнения  , мы получим
, мы получим 
Система свелась к одному существенному уравнению:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
 (*)
(*)
(два других ему пропорциональны). Беря, например, решение  ,
,  ,
,  уравнения (*), получим вектор
уравнения (*), получим вектор  , который определяет одно из бесчисленного множества главных направлений, соответствующих числу
, который определяет одно из бесчисленного множества главных направлений, соответствующих числу  .
.
С другой стороны, вектор  , определенный коэффициентами уравнения (*), дает третье главное направление (отвечающее числу
, определенный коэффициентами уравнения (*), дает третье главное направление (отвечающее числу  ). Умножая векторно
). Умножая векторно  на
на  , получим вектор
, получим вектор  , который также дает главное направление, отвечающее числу
, который также дает главное направление, отвечающее числу  (но отличное от ранее найденного и перпендикулярное к нему). Вместо последнего вектора удобнее взять
(но отличное от ранее найденного и перпендикулярное к нему). Вместо последнего вектора удобнее взять  . Нормируя найденные векторы и располагая их в надлежащем порядке, получим
. Нормируя найденные векторы и располагая их в надлежащем порядке, получим  ,
, 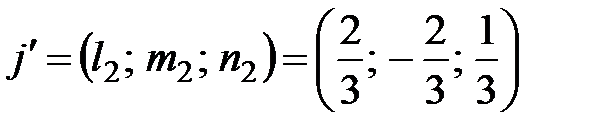 ,
,
 .
.
Отсюда имеем формулы искомого преобразования координат
 ,
, 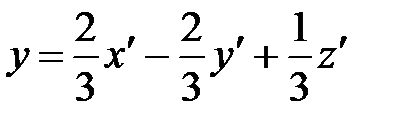 ,
,  .
.
Задача 5 Квадратичная форма  от трех переменных с матрицей
от трех переменных с матрицей

положительно определена, так как 
Задача 6 Квадратичная форма  от трех переменных с матрицей
от трех переменных с матрицей

является знакопеременной, так как 


Задача 7 Квадратичная форма 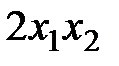 от двух переменных
от двух переменных
является знакопеременной, так как 

Задача 8 Дана квадратичная форма

1) Привести ее к каноническому виду методом Лагранжа, записав соответствующее преобразование переменных.
2) Привести ее к каноническому виду ортогональным преобразованием.
3) Проиллюстрировать закон инерции квадратичной формы на примерах преобразований, разобранных в п. 1) и 2).
Решение.
1) Коэффициент при 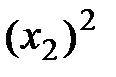 равен 3, т. е. отличен от нуля. Выделим в квадратичной форме члены, содержащие
равен 3, т. е. отличен от нуля. Выделим в квадратичной форме члены, содержащие 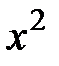 :
:  . Дополним это выражение до полного квадрата членами, не содержащими
. Дополним это выражение до полного квадрата членами, не содержащими 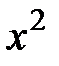 , и сразу вычтем добавленные члены. Тогда получим
, и сразу вычтем добавленные члены. Тогда получим 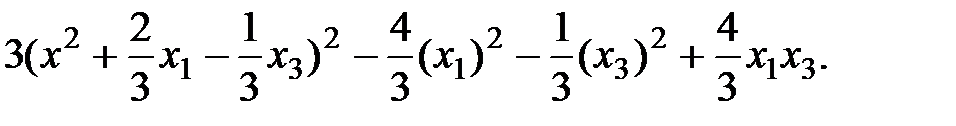
Введем обозначение  исходя из принципа:
исходя из принципа:  в квадратичной форме пропадает,
в квадратичной форме пропадает,  в квадратичной появляется. Приведя подобные члены, перепишем квадратичную форму:
в квадратичной появляется. Приведя подобные члены, перепишем квадратичную форму: 
К квадратичной форме  снова применим метод выделения полного квадрата. Выделим все члены, содержащие
снова применим метод выделения полного квадрата. Выделим все члены, содержащие  :
: 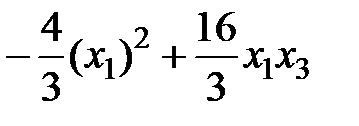 .
.
Дополним это выражение до полного квадрата членами, не содержащими  , т. е. приведем его к виду
, т. е. приведем его к виду  . Обозначим
. Обозначим  через
через  . Приведя подобные члены, перепишем исходную квадратичную форму:
. Приведя подобные члены, перепишем исходную квадратичную форму: 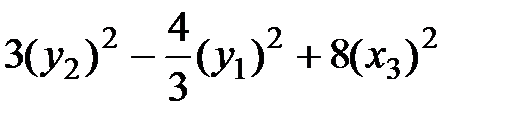 .
.
Выделять снова полный квадрат уже не надо, так как имеется только квадрат переменной 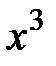 . Поэтому, введя обозначение
. Поэтому, введя обозначение  , получаем следующий канонический вид квадратичной формы:
, получаем следующий канонический вид квадратичной формы:  , где
, где 
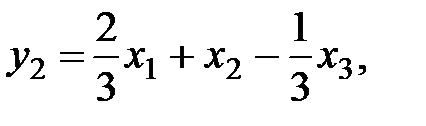

Запишем преобразование переменных в матричной форме:

Замечание 1. В результате применения метода Лагранжа всегда получается невырожденное линейное преобразование, приводящее квадратичную форму к каноническому виду.
Замечание 2. Если в записи квадратичной формы  отсутствует переменная
отсутствует переменная  , т. е.
, т. е.  то, записывая преобразование переменных, надо положить
то, записывая преобразование переменных, надо положить 
2) Запишем матрицу квадратичной формы:

В некотором евклидовом пространстве  с ортонормированным базисом
с ортонормированным базисом 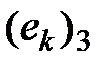 рассмотрим симметричный оператор
рассмотрим симметричный оператор  , для которого
, для которого  Построим для него ортонормированный собственный базис
Построим для него ортонормированный собственный базис 
Так как  то характеристическое уравнение запишется в виде
то характеристическое уравнение запишется в виде  Оно имеет решения
Оно имеет решения 
 Таким образом, получаем канонический вид квадратичной формы:
Таким образом, получаем канонический вид квадратичной формы: 
Построим теперь ортонормированный базис  Возьмем
Возьмем 
Тогда

Поэтому координаты  собственных векторов, соответствующих собственному значению
собственных векторов, соответствующих собственному значению  должны удовлетворять системе линейных уравнений
должны удовлетворять системе линейных уравнений

у которой 
 Следовательно ФСР этой системы состоит из одного решения, т. е. имеет, например, вид
Следовательно ФСР этой системы состоит из одного решения, т. е. имеет, например, вид 
Если 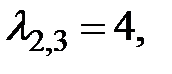 то
то  т. е. координаты
т. е. координаты  собственных векторов, соответствующих собственному значению 4, удовлетворяют системе линейных уравнений
собственных векторов, соответствующих собственному значению 4, удовлетворяют системе линейных уравнений  у которой
у которой 
 Поэтому, данная система эквивалентна уравнению
Поэтому, данная система эквивалентна уравнению  Значит, ФСР данной системы состоит из двух решений. Найдем их. Полагая сначала
Значит, ФСР данной системы состоит из двух решений. Найдем их. Полагая сначала  из последнего уравнения получим
из последнего уравнения получим  полагая затем
полагая затем  из того же уравнения имеем
из того же уравнения имеем 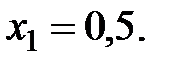 Таким образом, ФСР состоит из решений
Таким образом, ФСР состоит из решений 

Отметим, что 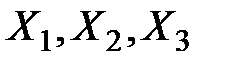 – столбцы из координат собственных векторов
– столбцы из координат собственных векторов  , которые образуют базис в
, которые образуют базис в  . При этом
. При этом  ортогонален
ортогонален  и
и  , так как
, так как  - собственный вектор, соответствующий собственному значению
- собственный вектор, соответствующий собственному значению  отличному от
отличному от 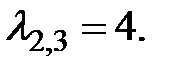 Следовательно, чтобы построить ортогональный базис из собственных векторов линейного оператора
Следовательно, чтобы построить ортогональный базис из собственных векторов линейного оператора  , надо ортогонализировать систему
, надо ортогонализировать систему  ,
,  .
.
Для этого положим 
 где
где  Отсюда получим,
Отсюда получим, 
Теперь собственные векторы  линейного оператора
линейного оператора  взаимно ортогональны. Нормируя эти векторы, получим ортонормированный базис
взаимно ортогональны. Нормируя эти векторы, получим ортонормированный базис 



Итак, ортогональное преобразование 
Приводит исходную квадратичную форму к каноническому виду:

3 ) В пунктах 1) и 2) одна и та же квадратичная форма двумя различными невырожденными преобразованиями приведена к двум различным каноническим видам. В каждом из них число положительных канонических коэффициентов равно 2, число отрицательных канонических коэффициентов равно 1.
|
|
