Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Линейные операторы, действующие в евклидовом пространстве

Среди линейных операторов, действующих в евклидовом пространстве, наибольший интерес представляют ортогональные и симметричные операторы.

Линейный оператор , действующий в евклидовом пространстве, называется ортогональным, если для любых из этого пространства выполняется равенство 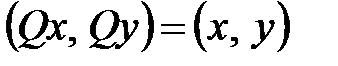. (80)

Теорема 10 В любом ортонормированном базисе матрица ортогонального оператора является ортогональной.

Линейный оператор , действующий в евклидовом пространстве, называют симметричным (самосопряженным), если для всех из этого пространства выполняется равенство . (81)

Теорема 11 В любом ортонормированном базисе матрица симметричного оператора является симметричной, т.е. .

Сформулируем свойства симметричного оператора.

1° Симметричный оператор, действующий в евклидовом пространстве , остается симметричным в любом инвариантном относительно линейного оператора подпространстве () евклидова пространства .

2° Все корней характеристического уравнения симметричного оператора – действительные числа и, следовательно, являются его собственными значениями.

3° Симметричный оператор всегда имеет собственные векторы.

4° Для симметричного оператора, действующего в евклидовом пространстве, существует ортонормированный собственный базис этого оператора.

5° Собственные векторы симметричного оператора, соответствующие различным собственным значениям, ортогональны между собой.