Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Билинейная форма. Связь с квадратичной формой. Приведение симметричной билинейной формы к каноническому виду

Говорят, что в линейном пространстве над числовым полем определена билинейная форма 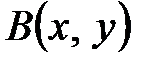, если любым из 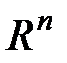ставится в соответствие определенное действительное число 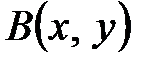, причем функция является линейной по каждому аргументу.

Если в линейном пространстве фиксирован базис и , (), то билинейная форма имеет вид , где 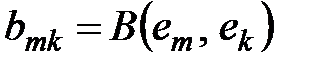. Матрица 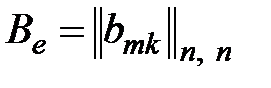называется матрицей билинейной формы в базисе .

Если в линейном пространстве фиксированы два базиса 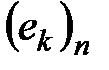, 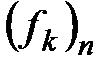и , то закон преобразования матрицы билинейной формы записывается в виде (84)

Билинейная форма называется симметричной, если 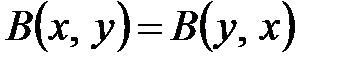для любых из .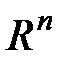

Теорема 6 В линейном пространстве билинейная форма симметрична тогда и только тогда, когда ее матрица симметрична.

Пусть задана билинейная форма 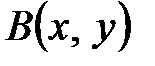в линейном пространстве . Рассмотрим функцию одного векторного аргумента: , . Если положить , то , . Из последней записи видно, что является квадратичной формой от переменных , которые интерпретируются как координаты элемента в базисе , т.е. . Каждой билинейной форме соответствует одна квадратичная форма. Каждую же квадратичную форму можно получить из бесконечного числа билинейных форм, среди которых имеется единственная симметричная билинейная форма.

Теорема 7 Для любой симметричной билинейной формы существует канонический базис , в котором эта форма имеет канонический вид , где , , .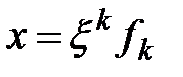

Пусть симметричная билинейная форма в базисе имеет матрицу . Тогда соответствующая ей квадратичная форма 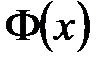имеет ту же матрицу . Для квадратичной формы существует линейное невырожденное преобразование , которое приводит эту квадратичную форму к каноническому виду 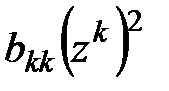. Канонический базис и канонический вид билинейной формы определяются соотношениями и .