
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическое занятие № 7
|
|
Задача 1 Является ли линейным оператор  , переводящий вектор
, переводящий вектор  в вектор
в вектор  , заданный координатами в том же базисе что и
, заданный координатами в том же базисе что и  . В случае линейности преобразования найти матрицу преобразования в том же базисе что и
. В случае линейности преобразования найти матрицу преобразования в том же базисе что и  .
.
а)  ; б)
; б)  ; в)
; в) 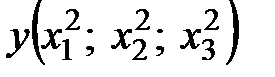 .
.
Решение.
Оператор  называется линейным оператором, если выполняются два условия: 1)
называется линейным оператором, если выполняются два условия: 1) 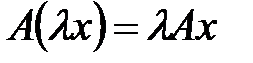 , если
, если  - любой вектор пространства,
- любой вектор пространства,  - любое число;
- любое число;
2)  , где
, где  и
и  - любые два вектора пространства
- любые два вектора пространства  .
.
а)  . Проверим выполнимость двух условий:
. Проверим выполнимость двух условий:
1)  ,
,

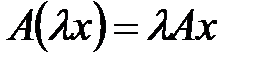 , следовательно, первое условие выполнено.
, следовательно, первое условие выполнено.
2)  .
.
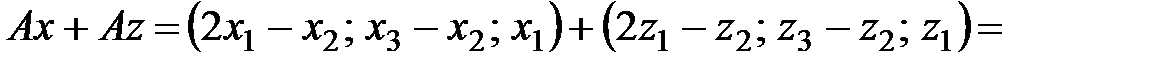
 .
.
Второе условие также выполняется. Таким образом, линейный оператор  , переводящий вектор
, переводящий вектор 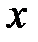 в вектор
в вектор  с координатами
с координатами  является линейным. Следовательно, матрица данного линейного оператора имеет вид:
является линейным. Следовательно, матрица данного линейного оператора имеет вид:
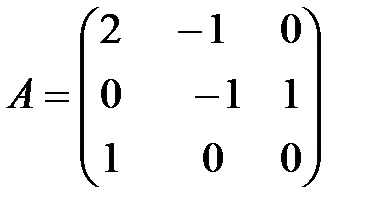
б) 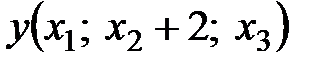
Проверим выполнимость двух условий:
1)  ,
,  , следовательно, первое условие выполняется.
, следовательно, первое условие выполняется.
2)  ,
,
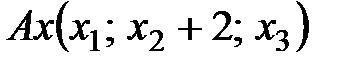
 ,
, 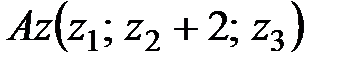
 .
.
Второе условие не выполняется и данный оператор  не является линейным.
не является линейным.
в) 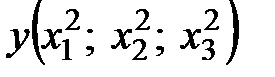
Проверим выполнимость двух условий:
1)  ,
,
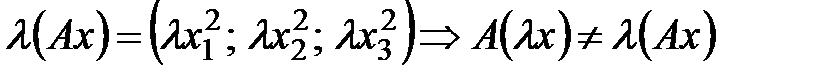 .
.
Первое условие не выполняется и оператор  не является линейным.
не является линейным.
Задача 2 Рассмотрим отображение  которое каждый вектор
которое каждый вектор  преобразует в его векторное произведение
преобразует в его векторное произведение  на орт
на орт  оси
оси  В силу свойств векторного произведения это отображение – линейный оператор. Найдем матрицу
В силу свойств векторного произведения это отображение – линейный оператор. Найдем матрицу  этого линейного оператора в (правом) ортонормированном базисе
этого линейного оператора в (правом) ортонормированном базисе 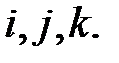
Решение.
Найдем образы базисных векторов и разложим их по тому же базису. Так как 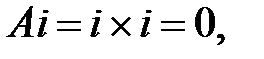 то первый столбец в матрице
то первый столбец в матрице  нулевой.
нулевой.
Второй столбец в матрице  :
:  .
.
Третий столбец в матрице  :
:  .
.
Итак, матрица 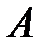 имеет вид:
имеет вид: 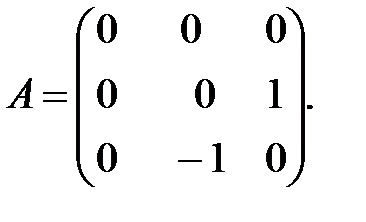
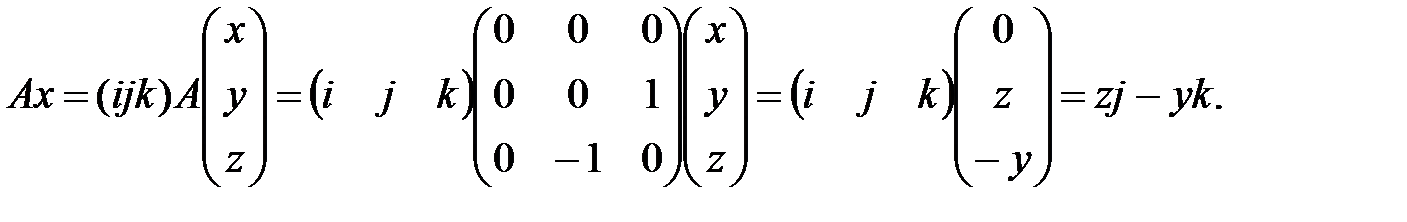
Задача 3 Матрица 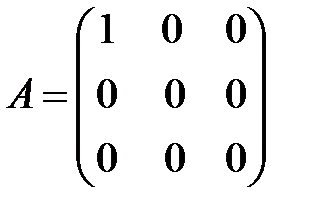
определяет линейное преобразование 


В прямоугольной системе координат  оно соответствует нахождению для произвольного вектора
оно соответствует нахождению для произвольного вектора  его составляющей (т.е. ортогональной проекции) по оси
его составляющей (т.е. ортогональной проекции) по оси 
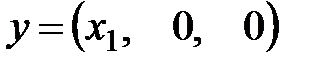
Задача 4 Матрица 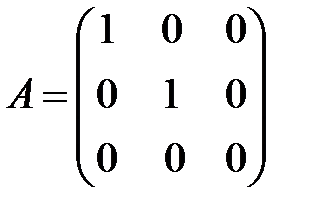
определяет линейное преобразование 


В прямоугольной системе координат  оно соответствует нахождению для произвольного вектора
оно соответствует нахождению для произвольного вектора  его составляющей (т.е. ортогональной проекции) на плоскость
его составляющей (т.е. ортогональной проекции) на плоскость 
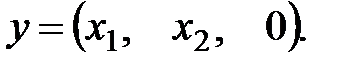
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Задача 5 Пусть  есть вращение на угол
есть вращение на угол  .
.
Решение.
Возьмем специальный базис  ,
,  (состоящий из единичных и взаимно перпендикулярных векторов). Тогда, если
(состоящий из единичных и взаимно перпендикулярных векторов). Тогда, если 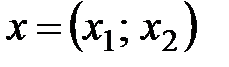 , то
, то  ,
,  , где
, где  ,
,  - полярные координаты конца вектора
- полярные координаты конца вектора  . Так как вектор
. Так как вектор  получается поворотом
получается поворотом  вокруг точки
вокруг точки  на угол
на угол  , то
, то  ,
, 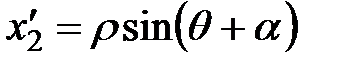 . Отсюда
. Отсюда
 ,
,
 ;
;
раскрывая скобки в правых частях этих равенств и полагая  ,
,  , найдем
, найдем
 ,
,
 .
.
Это и есть координатное представление вращения в базисе  ,
,  .
.
Матрица вращения имеет вид 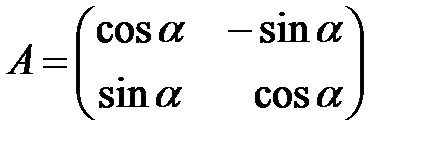 .
.
Задача 6 Пусть  - вращение на угол
- вращение на угол  ,
,  - вращение на угол
- вращение на угол  . Очевидно,
. Очевидно,  есть вращение на угол
есть вращение на угол  ; в данном случае
; в данном случае  .
.
Решение.
Возьмем специальный базис 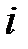 ,
,  ; тогда данные преобразования будут иметь соответственно матрицы
; тогда данные преобразования будут иметь соответственно матрицы
 ,
,  .
.
Применяя правило умножения матриц, получим
 .
.
Отсюда
 .
.
Этот результат можно было заранее предвидеть, так как  есть матрица вращения на угол
есть матрица вращения на угол  . В данном случае матрицы
. В данном случае матрицы 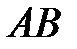 и
и  совпадают.
совпадают.
Задача 7 Пусть 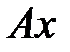 есть сжатие к оси
есть сжатие к оси  (т.е. в направлении оси
(т.е. в направлении оси  ) с коэффициентом
) с коэффициентом  ,
, 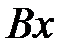 - сжатие к оси
- сжатие к оси  (т.е. в направлении оси
(т.е. в направлении оси  ) с коэффициентом
) с коэффициентом  . Матрицы этих преобразований соответственно будут
. Матрицы этих преобразований соответственно будут
 ,
,  ; умножая
; умножая  и
и 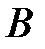 , получим
, получим  . Матрица такого вида называется диагональной. Таким образом, диагональная матрица отвечает произведению двух сжатий к координатным осям.
. Матрица такого вида называется диагональной. Таким образом, диагональная матрица отвечает произведению двух сжатий к координатным осям.
Задача 8 Построить ортонормированную систему векторов по линейно независимой системе 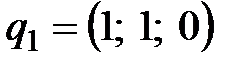 ,
,  ,
,  . Координаты векторов заданы в естественном базисе.
. Координаты векторов заданы в естественном базисе.
Решение.
Проверим систему векторов  на линейную независимость. Вектора
на линейную независимость. Вектора  линейно независимые, если их линейная комбинация
линейно независимые, если их линейная комбинация  при коэффициентах
при коэффициентах  Подставим значения
Подставим значения  в данное равенство, получим:
в данное равенство, получим:
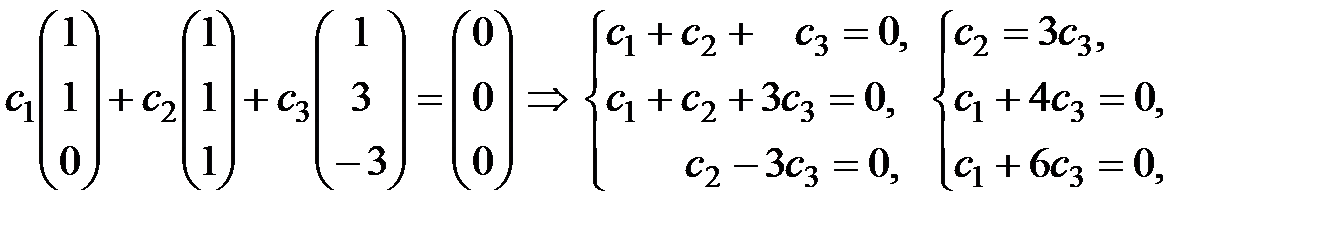
 линейно независимы.
линейно независимы.
1) Построим вспомогательную систему  - попарно ортогональные векторы:
- попарно ортогональные векторы:
а)  ;
;
б)  , где
, где  .
.
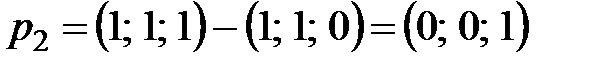 ;
;
в)  , где
, где  и
и  .
.
 .
.
2) Построим ортонормированную систему:
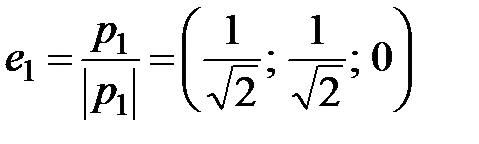 ;
;  ;
;  .
.
Ответ.  ,
,  ,
, 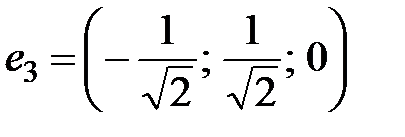
|
|
